题目内容
已知各项均为正数的等比数列{an}中，a2=1-a1，a4=9-a3，则a4+a5= ．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据题意可知公比q＞0，由等比数列的通项公式得a4+a3=（a2+a1）q2，代入数据求出q的值，再代入a4+a5=（a1+a2）q3，求出a4+a5的值．
解答：
解：因为数列{an}是各项均为正数的等比数列，
所以公比q＞0，
由a2=1-a1，a4=9-a3，得a2+a1=1，a4+a3=9，
则a4+a3=（a2+a1）q2，解得q=3，
所以a4+a5=（a1+a2）q3=27，
故答案为：27．
所以公比q＞0，
由a2=1-a1，a4=9-a3，得a2+a1=1，a4+a3=9，
则a4+a3=（a2+a1）q2，解得q=3，
所以a4+a5=（a1+a2）q3=27，
故答案为：27．
点评：本题考查等比数列的通项公式，以及整体代换的计算技巧，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
设奇函数f（x）在（0，+∞）上为单调递减函数，且f（2）=0，则不等式f（x）＜0的解集为（ ）
| A、（-∞，-2）∪（0，2） |
| B、（-∞，-2）∪（2，+∞） |
| C、（-2，0）∪（2，+∞） |
| D、（-2，0）∪（0，2） |
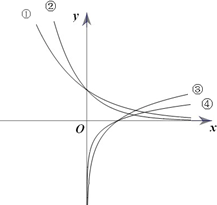如图，设实数a，b，c，d＞0，且不等于1，曲线①，②，③，④分别表示函数y=ax，y=bx，y=logcx，y=logdx在同一坐标系中的图象，则a，b，c，d的大小顺序为