题目内容
13.设函数f(x)=|x+2|+|x-2|,x∈R.(Ⅰ)求不等式f(x)≤6的解集;
(Ⅱ)若关于x的方程f(x)=a|x-1|恰有两个不同的实数根,求a的取值范围.
分析 (Ⅰ)根据绝对值的意义,求得不等式f(x)≤6的解集.
(Ⅱ)函数f(x)的图象(图中红色部分)与直线 y=a|x-1|有2个不同的交点,数形结合可得a的范围.
解答 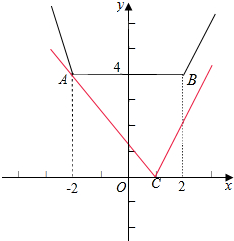 解:(Ⅰ)函数f(x)=|x+2|+|x-2|表示数轴上的x
解:(Ⅰ)函数f(x)=|x+2|+|x-2|表示数轴上的x
对应点到-2、2对应点的距离之和,
而3和-3对应点到-2、2对应点的距离之和正好等于6,
故不等式f(x)≤6的解集为 {x|-3≤x≤3 }.
(Ⅱ)∵f(x)=|x+2|+|x-2|=$\left\{\begin{array}{l}{-2x,x<-2}\\{4,-2≤x≤2}\\{2x,x>2}\end{array}\right.$,
∴f(x)≥4,
若关于x的方程f(x)=a|x-1|恰有两个不同的实数根,
则函数f(x)的图象与直线 y=a|x-1|(图中红色部分)
有2个不同的交点,如图所示:
由于A(-2,4)、B(2,4)、C(1,0),
∴-2<-a<KCA,或 a≥KCB,
即-2<-a<-$\frac{4}{3}$,或a≥4,
求得 $\frac{4}{3}$<a<2,或a≥4.
点评 本题主要绝对值的意义,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
3.已知集合A,B,定义A-B={x|x∈A且x∉B},A+B={x|x∈A或x∈B},则对于集合M,N下列结论一定正确的是( )
| A. | M-(M-N)=N | B. | (M-N)+(N-M)=∅ | C. | (M+N)-M=N | D. | (M-N)∩(N-M)=∅ |
4.若f(x)=3x+5,则f-1(x)的定义域是( )
| A. | (0,+∞) | B. | (5,+∞) | C. | (8,+∞) | D. | (-∞,+∞) |
18.函数y=$\sqrt{k{x}^{2}-6kx+k+8}$的定义域为一切实数,则k的取值范围是( )
| A. | k>0或k≤-9 | B. | k≥1 | C. | -9≤k≤1 | D. | 0≤k≤1 |
2.已知点P为△ABC所在的平面内一点,且$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$=$\overrightarrow{PC}$•$\overrightarrow{PA}$=-1,则△ABC的面积为( )
| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
17.已知命题p:?x∈R,ex+x3+2x2+4≠0,则?p为( )
| A. | ?x0∈R,使得lnx0+x03+2x02+4=0 | B. | ?x0∈R,使得ex0+x03+2x02+4≠0 | ||
| C. | ?x∈R,使得ex+x3+2x2+4=0 | D. | ?x0∈R,使得ex0+x03+2x02+4=0 |