Question

某厂生产甲，乙两种产品，生产每吨产品所需的劳动力、钢材以及耗电量如下表：

产品品种	劳动力（单位：个）	钢材（单位：千克）	电（单位：千瓦）
甲产品	3	9	4
乙产品	10	4	5

已知生产甲产品的利润是每吨3万元，生产乙产品的利润是每吨5万元，现因条件限制，该厂仅有劳动力300个，钢材360千克，并且供电局只能供电200千瓦，试问该厂如何安排生产，才能获得最大利润．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：根据条件建立约束条件，利用线性规划的知识进行求解即可．

解答： 解：设安排生产甲乙两种产品分别为x顿，y顿，利润为z万元，
则由题意得约束条件为

3x+10y≤300 9x+4y≤360 4x+5y≤200 x≥0，y≥0

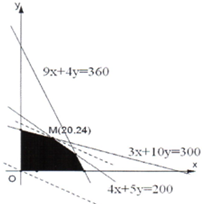
，目标函数为z=3x+5y，
由z=3x+5y得y=-

3

5

x+

z

5

，
平移直线y=-

3

5

x+

z

5

，则由图象可知当直线y=-

3

5

x+

z

5

经过点M（20，24）时直线y=-

3

5

x+

z

5

的截距最大，
此时z=3×20+5×24=180万元，
答：安排生产甲乙两种产品分别为20顿，24顿，才能获得最大利润．最大利润为180万元．

点评：本题主要考查生活中的优化问题，利用线性规划是解决本题的关键．