题目内容
设等比数列{an}的公比q=2，前n项和为Sn，则
=（ ）
| S4 |
| S2 |
A、
| ||
| B、5 | ||
| C、4 | ||
| D、2 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：设出等比数列的首项，然后把S4，S2用首项表示，代入
得答案．
| S4 |
| S2 |
解答：
解：设等比数列{an}的首项为a1，
又公比q=2，
∴S4=
=15a1，
S2=a1+2a1=3a1，
∴
=
=5．
故选：B．
又公比q=2，
∴S4=
| a1(1-24) |
| 1-2 |
S2=a1+2a1=3a1，
∴
| S4 |
| S2 |
| 15a1 |
| 3a1 |
故选：B．
点评：本题考查了等比数列的通项公式，考查了等比数列的前n项和，是基础题．
练习册系列答案
相关题目
某厂生产甲，乙两种产品，生产每吨产品所需的劳动力、钢材以及耗电量如下表：己知函数f（x）=tx，g（x）=（2-t）x2-4x+l．若对于任一实数x0，函数值f（x0）与g（x0）中至少有一个为正数，则实数t的取值范围是（ ）
| A、（-∞，-2）∪（0，2] |
| B、（-2，0）∪（-2，2] |
| C、（-2，2] |
| D、（0，+∞） |
某工厂去年产值为a，计划今后5年内每年比上年产值增加10%，则从今年起到第5年，这个厂的总产值为（ ）
| A、1.14a |
| B、11×（1.15-1）a |
| C、1.15a |
| D、10×（1.16-1）a |
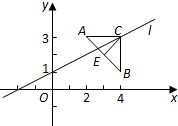如图，已知点A（2，3），B（4，1），△ABC是以AB为底边的等腰三角形，点C在直线l：x-2y+2=0上．
某商场为经营一批每件进价是10元的小商品，对该商品进行为期5天的市场试销．下表是市场试销中获得的数据．