题目内容
8.将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{4}$个单位长度,所得函数图象的一条对称轴方程是( )| A. | x=$\frac{2}{3}$π | B. | x=-$\frac{1}{12}$π | C. | x=$\frac{1}{3}$π | D. | x=$\frac{5}{12}$π |
分析 根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得所得函数图象的一条对称轴方程.
解答 解:将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{4}$个单位长度,可得y=sin(2x+$\frac{π}{2}$-$\frac{π}{3}$)=sin(2x+$\frac{π}{6}$)的图象,
令2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,可得所得函数图象的对称轴方程为x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
令k=1,可得所得函数图象的一条对称轴方程为x=$\frac{2π}{3}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
15.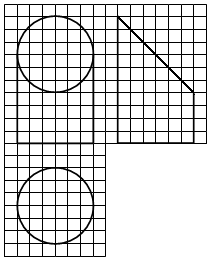 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
17.在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
| A. | a=2b | B. | b=2a | C. | A=2B | D. | B=2A |
18.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.
(I)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
| 连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
| 甲 | 70 | 5 | 60 |
| 乙 | 60 | 5 | 25 |
(I)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?