题目内容
17.已知曲线y=$\sqrt{x}$与y=$\frac{8}{x}$的交点为P,两曲线在点P处的切线分别为l1,l2,则切线l1,l2及y轴所围成的三角形的面积为6.分析 先联立方程,求出两曲线交点,再分别对y=$\sqrt{x}$与y=$\frac{8}{x}$求导,利用导数,求出两曲线在交点处的切线斜率,利用点斜式求出切线方程,找到两切线与y轴交点,最后用面积公式计算面积即可.
解答 解:曲线y=$\sqrt{x}$与y=$\frac{8}{x}$,它们的交点坐标是P(4,2),
y=$\sqrt{x}$的导数为y′=$\frac{1}{2\sqrt{x}}$,在P处的切线的斜率为$\frac{1}{4}$,
y=$\frac{8}{x}$的导数为y′=-$\frac{8}{{x}^{2}}$,在P处的切线的斜率为-$\frac{1}{2}$,
两条切线方程分别是y=$\frac{1}{4}$x+1和y=-$\frac{1}{2}$x+4,
x=0时,y=1和y=4,
两切线的交点为(4,2),
于是三角形三顶点坐标分别为 (0,1);(0,4);(4,2),
它们与y轴所围成的三角形的面积是$\frac{1}{2}$×(4-1)×4=6.
故答案为:6.
点评 本题考查了利用导数求切线方程,注意运用直线方程,求交点,考查面积公式的运用,属于中档题.

练习册系列答案
相关题目
6.函数f(x)是R上的偶函数,且在(0,+∞)上单调增,则f(-5)和f(3)的大小关系是( )
| A. | f(-5)>f(3) | B. | f(-5)=f(3) | C. | f(-5)<f(3) | D. | 无法确定 |
7.在△ABC中,点M在边BC上,且2$\overrightarrow{BM}$=3$\overrightarrow{MC}$,E在边AC上,且$\overrightarrow{EC}$=3$\overrightarrow{AE}$,则向量$\overrightarrow{EM}$-$\overrightarrow{AB}$=( )
| A. | $\frac{7}{20}$$\overrightarrow{AC}$-$\frac{3}{5}$$\overrightarrow{AB}$ | B. | $\frac{7}{20}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$ | C. | $\frac{2}{5}$$\overrightarrow{AC}$-$\frac{3}{5}$$\overrightarrow{AB}$ | D. | $\frac{1}{3}$$\overrightarrow{AC}$+$\frac{1}{5}$$\overrightarrow{AB}$ |
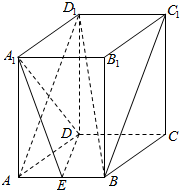 长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点. 如图,在直三棱柱 ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱 ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.