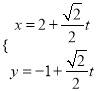Question

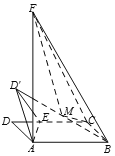
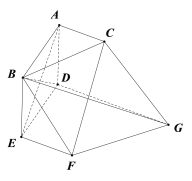
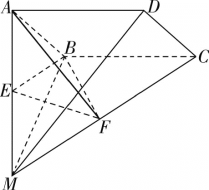
【题目】如图，四棱锥M－ABCD中，MB⊥平面ABCD，四边形ABCD是矩形，AB＝MB，E、F分别为MA、MC的中点．

（1）求证：平面BEF⊥平面MAD；

（2）若，求三棱锥E－ABF的体积．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）先证明BE⊥平面MAD，再证平面BEF⊥平面MAD；（2）利用体积变换求三棱锥E－ABF的体积．

（1）因为MB⊥平面ABCD，所以MB⊥AD，

又因为四边形ABCD是矩形，所以AD⊥AB，

因为AB∩MB＝B，所以AD⊥平面MAB，

因为BE平面MAB，所以AD⊥BE，

又因为AB＝MB，E为MA的中点，

所以BE⊥MA，因为MA∩AD＝A，

所以BE⊥平面MAD，

又因为BE平面BEF，

所以平面BEF⊥平面MAD．

（2）因为AD∥BC，所以BC⊥面MAB，又因为F为MC的中点，

所以F到面MAB的距离，

又因为MB⊥平面ABCD，AB＝MB＝，E为MA的中点，

所以，

所以．