题目内容
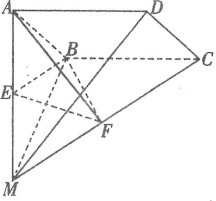
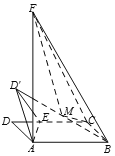
【题目】如图,已知矩形ABCD,![]() ,
,![]() ,AF⊥平面ABC,且
,AF⊥平面ABC,且![]() .E为线段DC上一点,沿直线AE将△ADE翻折成
.E为线段DC上一点,沿直线AE将△ADE翻折成![]() ,M为
,M为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 体积的最小值是________.
体积的最小值是________.
【答案】![]()
【解析】
首先分析出![]() ,即求棱锥
,即求棱锥![]() 体积的最小值即求点
体积的最小值即求点![]() 到平面
到平面![]() 的距离的最小值,转化为求点
的距离的最小值,转化为求点![]() 到平面
到平面![]() 距离的最小值,由条件确定点
距离的最小值,由条件确定点![]() 的运动轨迹为以
的运动轨迹为以![]() 为球心,半径为1的球面的一部分,然后根据图象分析点
为球心,半径为1的球面的一部分,然后根据图象分析点![]() 到平面
到平面![]() 距离的最小值.
距离的最小值.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,
所以![]() ,
,
所以求棱锥![]() 体积的最小值即求点
体积的最小值即求点![]() 到平面
到平面![]() 的距离的最小值,
的距离的最小值,
因为点![]() 是
是![]() 的中点,
的中点,
所以点![]() 到平面
到平面![]() 的距离是点
的距离是点![]() 到平面
到平面![]() 距离的一半,
距离的一半,
因为![]() ,随着点
,随着点![]() 在线段
在线段![]() 上移动,
上移动,
点![]() 的运动轨迹为以
的运动轨迹为以![]() 为球心,半径为1的球面的一部分,
为球心,半径为1的球面的一部分,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,并且交于
,并且交于![]() ,
,
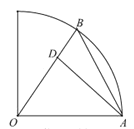
所以如图,过点![]() 作
作![]() ,即
,即![]() 平面
平面![]() ,
,
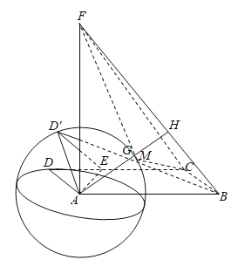
当![]() 为
为![]() 与球面的交点
与球面的交点![]() 时,
时,![]() 到平面
到平面![]() 的距离最小,
的距离最小,
此时点![]() 在线段
在线段![]() 上,
上,
根据![]() ,
,
可得![]() ,此时
,此时![]() ,
,
即![]() 到平面
到平面![]() 的距离的最小值是
的距离的最小值是![]() ,那么点
,那么点![]() 到平面
到平面![]() 距离的最小值是
距离的最小值是![]() ,
,
所以三棱锥![]() 体积的最小值是
体积的最小值是![]() .
.
故答案为:![]()

练习册系列答案
相关题目