Question

【题目】已知动圆Q经过定点，且与定直线相切（其中a为常数，且）.记动圆圆心Q的轨迹为曲线C.

（1）求C的方程，并说明C是什么曲线？

（2）设点P的坐标为，过点P作曲线C的切线，切点为A，若过点P的直线m与曲线C交于M，N两点，则是否存在直线m，使得？若存在，求出直线m斜率的取值范围；若不存在，请说明理由.

Answer 1

【答案】（1），抛物线；（2）存在，.

【解析】

（1）设，易得，化简即得；

（2）利用导数几何意义可得，要使，只需.

联立直线m与抛物线方程，利用根与系数的关系即可解决.

（1）设，由题意，得，化简得，

所以动圆圆心Q的轨迹方程为，

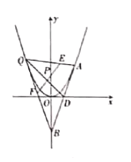
它是以F为焦点，以直线l为准线的抛物线.

（2）不妨设.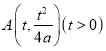

因为，所以，

从而直线PA的斜率为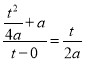，解得，即，

又，所以轴.

要使，只需.

设直线m的方程为，代入并整理，

得.

首先，，解得或.

其次，设，，

则，.

.

故存在直线m，使得，

此时直线m的斜率的取值范围为.