题目内容
16.已知函数f(x)=a-$\frac{2}{{2}^{x}+1}$(1)求证:f(x)为增函数;
(2)若f(x)为奇函数,求f(x)的值域;
(3)在(2)成立的情况下,若g(x)=xf(x)-2m+5,在定义域内总有g(x)≥0成立,求m的取值范围.
分析 (1)根据函数单调性的定义进行证明,
(2)根据函数奇偶性的性质,结合指数函数单调性的性质进行求解.
(3)根据指数函数单调性的性质进行求解.
解答 解:(1)∵f(x)的定义域为R,不妨设:x1<x2
则$f({x_1})-f({x_2})=a-\frac{2}{{{2^{x_1}}+1}}-a+\frac{2}{{{2^{x_2}}+1}}$=$\frac{{2•({2^{x_1}}-{2^{x_2}})}}{{(1+{2^{x_1}})(1+{2^{x_2}})}}$,
∵x1<x2,∴${2^{x_1}}-{2^{x_2}}<0,(1+{2^{x_1}})(1+{2^{x_2}})>0$,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数.…(3分)
(2)∵f(x)为奇函数,∴f(-x)=-f(x),
即$a-\frac{2}{{{2^{-x}}+1}}=-a+\frac{2}{{{2^x}+1}}$,解得:a=1.∴$f(x)=1-\frac{2}{{{2^x}+1}}$.…(5分)
$f(x)=1-\frac{2}{{{2^x}+1}}$,
∵2x+1>1,∴$0<\frac{2}{{{2^x}+1}}<2$,∴$-2<-\frac{2}{{{2^x}+1}}<0$,∴-1<f(x)<1
∴f(x)的值域为(-1,1).…(8分)
(3)在定义域内总有g(x)≥0成立,即xf(x)≥2m-5在R内总成立,
结合(2)当x≥0时,2x+1≥2,$0<\frac{2}{{{2^x}+1}}≤1$$0≤1-\frac{2}{{{2^x}+1}}<1$,即f(x)≥0,
∴xf(x)≥0
同理:当x<0时,f(x)<0,∴xf(x)>0,
∴xf(x)≥0在R内总成立,
∴0≥2m-5,$m≤\frac{5}{2}$
∴当$m≤\frac{5}{2}$时,定义域内总有g(x)≥0成立. …(12分)
点评 本题主要考查函数奇偶性和单调性的判断和证明,利用定义法以及转化法是解决本题的关键.综合考查函数的性质.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 9 | C. | 10 | D. | 18 |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
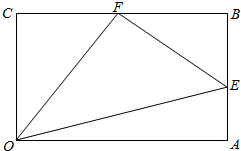 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.