题目内容
13.已知函数f(x)=logax(a>0且a≠1).(1)若a=3,f($\frac{27}{x}$)=-5,求x的值;
(2)若f(3a-1)>f(a),求实数a的取值范围.
分析 (1)由f($\frac{27}{x}$)=-5列出方程,根据对数得运算法则解出x;
(2)根据a的不同范围讨论f(x)的单调性,利用函数的单调性列出不等式解出a.
解答 解:(1)f($\frac{27}{x}$)=log3($\frac{27}{x}$)=-5,∴$\frac{27}{x}$=3-5,∴x=$\frac{27}{{3}^{-5}}$=$\frac{{3}^{3}}{{3}^{-5}}$=38.
(2)①若a>1,则f(x)在(0,+∞)上是增函数,∴3a-1>a>0,解得a>1.
②若0<a<1,则f(x)在(0,+∞)上是减函数,∴0<3a-1<a,解得$\frac{1}{3}$<a<$\frac{1}{2}$,
综上,a的取值范围是($\frac{1}{3}$,$\frac{1}{2}$)∪(1,+∞).
点评 本题考查了对数得运算性质,对数函数的单调性及应用,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤10}\\{-\frac{x}{2}+6,x>10}\end{array}\right.$,若函数y=f2(x)-2bf(x)+b-$\frac{2}{9}$有6个零点,则b的取值范围是( )
| A. | ($\frac{2}{9}$,$\frac{1}{3}$)∪($\frac{2}{3}$,$\frac{7}{9}$) | B. | (-∞,$\frac{1}{3}$)∪($\frac{2}{3}$,+∞) | C. | (0,$\frac{1}{3}$)∪($\frac{2}{3}$,1) | D. | ($\frac{2}{9}$,$\frac{7}{9}$) |
19.有红、黄、蓝旗各3面,每次升1面、2面、3面在某一旗杆上纵向排列,共可以组成( )种不同的信号.
| A. | 27 | B. | 30 | C. | 36 | D. | 39 |
1.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e=$\frac{\sqrt{13}}{2}$,则它的渐近线方程为( )
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{3}{2}$x | C. | y=±$\frac{9}{4}$x | D. | y=±$\frac{4}{9}$x |
8.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的两点A,B,若|AF|=4|FB|,则k的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{3}{4}\sqrt{2}$ | C. | $\frac{{\sqrt{17}}}{4}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
18.已知a=ln0.2,b=20.3,c=0.30.2,则实数a,b,c的大小关系为( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | b>a>c |
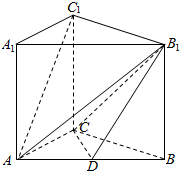 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.