题目内容
19.已知直线x+y=a与圆O:x2+y2=8交于A,B两点,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则实数a的值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$或-2$\sqrt{2}$ | D. | 4或-4 |
分析 根据条件可以得到OA⊥OB,从而△OAB为等腰直角三角形,∠AOB=90°,并且$OA=OB=2\sqrt{2}$,从而便可求出圆心O到直线x+y=a的距离为2,即得到$\frac{|a|}{\sqrt{2}}=2$,从而可得出实数a的值.
解答 解:由$\overrightarrow{OA}•\overrightarrow{OB}=0$得,$\overrightarrow{OA}⊥\overrightarrow{OB}$;
∴△OAB为等腰直角三角形;
∴圆心到直线的距离等于d=2;
∴由点到直线距离公式得,$\frac{|a|}{\sqrt{2}}=2$,$a=±2\sqrt{2}$.
故选C.
点评 考查向量垂直的充要条件,圆的标准方程,直角三角形斜边的中线等于斜边的一半,以及点到直线的距离公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在正三棱锥S-ABC中,SA⊥SB,AB=$\sqrt{2}$,则正三棱谁S-ABC外接球的体积为( )
| A. | 3π | B. | 2$\sqrt{3}$π | C. | $\sqrt{3}$π | D. | $\frac{\sqrt{3}}{2}$π |
11.已知集合A={-1,0,1},集合B={x|1≤2x≤4},则A∩B=( )
| A. | {-1,0,1} | B. | {1} | C. | {-1,1} | D. | {0,1} |
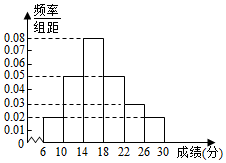 某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.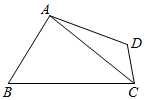 如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.
如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.