题目内容
9.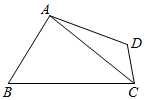 如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.
如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.(1)求sin∠ACB的值;
(2)若$∠BCD=\frac{3π}{4}$,CD=1,求△ACD的面积.
分析 (1)在△ABC中,由已知及余弦定理,比例的性质即可解得BC=3,AB=2,由正弦定理即可解得sin∠ACB的值
(2)由(1)及余弦定理可求cos∠ACB,利用两角差的正弦函数公式可求sin∠ACD的值,利用三角形面积公式即可计算得解.
解答  解:(1)∵∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$,可得:AB=$\frac{2BC}{3}$,
解:(1)∵∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$,可得:AB=$\frac{2BC}{3}$,
∴在△ABC中,由余弦定理AC2=AB2+BC2-2AB•BC•cos∠ABC,可得:7=$\frac{4B{C}^{2}}{9}$+BC2-$\frac{2B{C}^{2}}{3}$,
∴解得:BC=3,AB=2,
∴由正弦定理可得:sin∠ACB=$\frac{AB•sin∠ABC}{AC}$=$\frac{2×\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
(2)∵由(1)及余弦定理可得:
cos∠ACB=$\frac{A{C}^{2}+B{C}^{2}-A{B}^{2}}{2•AC•BC}$=$\frac{7+9-4}{2×\sqrt{7}×3}$=$\frac{2\sqrt{7}}{7}$,
∴sin$∠ACD=sin(\frac{3π}{4}-∠ACB)$=$\frac{\sqrt{2}}{2}$(cos∠ACB+sin∠ACB)
=$\frac{\sqrt{2}}{2}$($\frac{2\sqrt{7}}{7}$+$\frac{\sqrt{21}}{7}$),
∴S△ACD=$\frac{1}{2}$AC•CD•sin∠ACD=$\frac{1}{2}×\sqrt{7}×$1×$\frac{\sqrt{2}}{2}$×($\frac{2\sqrt{7}}{7}$+$\frac{\sqrt{21}}{7}$)=$\frac{2\sqrt{2}+\sqrt{6}}{4}$.
点评 本题主要考查了余弦定理,比例的性质,正弦定理,两角差的正弦函数公式,三角形面积公式以及特殊角的三角函数值在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.

| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$或-2$\sqrt{2}$ | D. | 4或-4 |
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | {x|0<x<3} | B. | {x|-1<x<0} | C. | {x|-2<x<0} | D. | {x|-3<x<3} |