题目内容
7.设x,y,z∈R,若x+2y+z=4.(1)求x2+y2+z2的最小值;
(2)求x2+(y-1)2+z2的最小值.
分析 利用柯西不等式即可求解.
解答 解:(1)由柯西不等式,
得:(x2+y2+z2)(12+22+12)≥(x+2y+z)2
即:6(x2+y2+z2)≥42,
∴x2+y2+z2≥$\frac{8}{3}$,当且仅当$\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$时等号成立,
故:x2+y2+z2的最小值为$\frac{8}{3}$.
(2)由柯西不等式,
得:[x2+(y-1)2+z2](12+22+12)≥(x+2y-2+z)2.
即:6[x2+(y-1)2+z2]≥4,
∴x2+(y-1)2+z2≥$\frac{2}{3}$,当且仅当$\frac{x}{1}=\frac{y-1}{2}=\frac{z}{1}$时等号成立,
故:x2+(y-1)2+z2的最小值为$\frac{2}{3}$.
点评 本题考查了柯西不等式的运用能力,考查学生的计算能力.属于基础题.

练习册系列答案
相关题目
20.在△ABC中,若$\overrightarrow{AB}•(\overrightarrow{CA}+\overrightarrow{CB})=0$,且$\overrightarrow{BA}•\overrightarrow{BC}={\overrightarrow{BC}^2}$,则$\overrightarrow{AB}与\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
2.已知一个几何体的三视图如图所示,则该几何体的体积为( )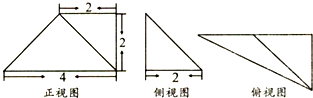

| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
19.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足${k_1}{k_2}=\frac{2}{3}$,则l一定过点( )
| A. | (-3,0) | B. | (3,0) | C. | (-1,3) | D. | (-2,0) |
15.函数f(x)是定义在区间(0,+∞)上的可导函数,其导函数为f′(x),且满足xf′(x)+2f(x)>0,则不等式$\frac{(x+2016)f(x+2016)}{5}<\frac{5f(5)}{x+2016}$的解集为( )
| A. | {x>-2011} | B. | {x|x<-2011} | C. | {x|-2011<x<0} | D. | {x|-2016<x<-2011} |
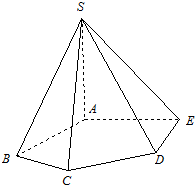 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°