题目内容
15.函数f(x)是定义在区间(0,+∞)上的可导函数,其导函数为f′(x),且满足xf′(x)+2f(x)>0,则不等式$\frac{(x+2016)f(x+2016)}{5}<\frac{5f(5)}{x+2016}$的解集为( )| A. | {x>-2011} | B. | {x|x<-2011} | C. | {x|-2011<x<0} | D. | {x|-2016<x<-2011} |
分析 根据条件,构造函数,利用函数的单调性和导数之间的关系,将不等式进行转化即可得到结论
解答 解:构造函数g(x)=x2f(x),g′(x)=x(2f(x)+xf′(x));
当x>0时,
∵2f(x)+xf′(x)>0,
∴g′(x)>0,
∴g(x)在(0,+∞)上单调递增,
∵不等式$\frac{(x+2016)f(x+2016)}{5}<\frac{5f(5)}{x+2016}$,
∴x+2016>0时,即x>-2016时,
∴(x+2016)2f(x+2016)<52f(5),
∴g(x+2016)<g(5),
∴x+2016<5,
∴-2016<x<-2011,
故选:D.
点评 本题主要考查不等式的解法,利用条件构造函数,利用函数单调性和导数之间的关系是解决本题的关键

练习册系列答案
相关题目
4.若A,B,C是函数f(x)=ex+x图象上横坐标成等差数列的三个点,给出以下判断:①△ABC可能是直角三角形;②△ABC一定是钝角三角形;③△ABC可能是等腰三角形;④△ABC一定不是等腰三角形.其中,正确的判断是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
20.已知函数f(x)对?x∈R都有f(x)=f(4-x),且其导函数f′(x)满足当x≠2时,(x-2)f′(x)>0,则当2<a<4时,有( )
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
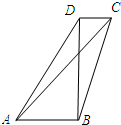 如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )
如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )