题目内容
12.设函数f(x)=x2+ax-lnx,其中实数a为常数.(1)若a=2,求曲线y=f(x)在点P(1,f(1))处的切线方程;
(2)若函数g(x)=$\frac{f(x)}{{e}^{x}}$在区间(0,1]上是减函数,其中e为自然对数的底数,求a的取值范围.
分析 (1)欲求在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)先求导,再构造函数设h(x)=-x2+(2-a)x+a-$\frac{1}{x}$+lnx 由h'(x)在(0,1]上是减函数,可得h'(x)≥h'(1)=2-a,通过研究2-a的正负可判断h(x)的单调性,进而可得函数F(x)的单调性,可求参数的取值范围
解答 解:(1)a=2,y=f(x)=x2+2x-lnx,
∴f′(x)=2x+2-$\frac{1}{x}$,
∴f′(1)=2+2-1=3,f(1)=1+2-0=3,
∴曲线在点(1,f(1))处的切线方程为:y-3=3×(x-1),即y=3x.
(2)g(x)=$\frac{f(x)}{{e}^{x}}$,f(x)=x2+ax-lnx,
∴g′(x)=$\frac{-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx}{{e}^{x}}$,
设h(x)=-x2+(2-a)x+a-$\frac{1}{x}$+lnx,
则h′(x)=-2x+$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2-a,
易知h′(x)在(0,+∞)上是减函数,
从而h′(x)≥h′(1)=2-a,
①当2-a≥0时,即a≤2时,h′(x)≥0,h(x)在(0,1)上是增函数
∵h(1)=0,
∴h(x)≤0在(0,1]上恒成立,
即g′(x)≤0区间(0,1]上是单调递减函数,
∴a≤2满足题意,
②当2-a<0时,即a>2时,设函数h′(x)的唯一零点为x0,则h(x)在(0,x0)上单调递增,在(x0,1)单调递减,
又∵h(1)=0,
∴h(x0)>0,
又∵h(e-a)<0,
∴h(x)在(0,1)内有唯一一个零点m,
当x∈(0,m)时,h(x)<0,
当x∈(m,1)时,h(x)>0,从而f(x)在(0,m)上单调递减,在(m,1)上单调递增,与在区间(0,1]上是减函数矛盾,
∴a>2不合题意,
综合所述a的取值范围为(-∞,2].
点评 考查学生利用导数研究函数的单调能力,函数单调性的判定,以及导数的运算,试题具有一定的综合性,属于中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案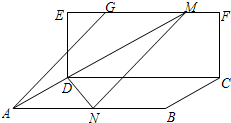 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
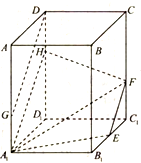 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.