Question

已知函数f（x）=

ex-1，x≥0 -x2-2x，x＜0

，若关于x的方程f（x）=|x-a|有三个不同的实根，则实数a的取值范围是（　　）

• A、（-

  9

  4

  ，0）
• B、（0，

  1

  4

  ）
• C、（-

  9

  4

  ，

  1

  4

  ）
• D、（-

  9

  4

  ，0）或（0，

  1

  4

  ）

Answer 1

考点：根的存在性及根的个数判断

专题：计算题,作图题,函数的性质及应用

分析：由题意，关于x的方程f（x）=|x-a|有三个不同的实根转化为函数图象的交点问题，从而作图解答．

解答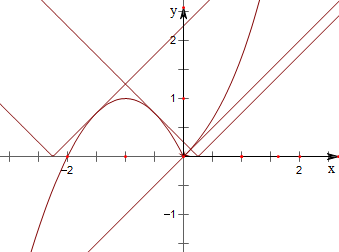： 解：直线y=x-a与函数f（x）=e^x-1的图象在x≥0处有一个切点，
切点坐标为（0，0）；此时a=0；
直线y=|x-a|与函数y=-x²-2x的图象在x＜0处有两个切点，
切点坐标分别是（-

1

2

，

3

4

）和（-

3

2

，

3

4

）；
此时相应的a=

1

4

，a=-

9

4

；
观察图象可知，方程f（x）=|x-a|有三个不同的实根时，
实数a的取值范围是
（-

9

4

，0）或（0，

1

4

）；
故选D．

点评：本题考查了函数的图象与方程的根的关系，属于中档题．