题目内容
 如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )
如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )| A、(-2,-1) | ||
B、[
| ||
C、[-1,-
| ||
D、(-1,-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:先根据约束条件的可行域,利用目标函数几何意义求最值,z=ax-y表示直线在y轴上的截距的相反数,a表示直线的斜率,只需求出a的取值范围时,可行域直线在y轴上的截距最优解即可.
解答:
解:由可行域可知,直线BP的斜率=
=-
,
直线AP的斜率=
=-1,
当直线z=ax-y的斜率介于BP与AP之间时,P(2,2)是该目标函数z=ax-y的唯一最优解,
所以a∈(-1,-
),
故选:D.
| 2-3 |
| 2-0 |
| 1 |
| 2 |

直线AP的斜率=
| 2-0 |
| 2-4 |
当直线z=ax-y的斜率介于BP与AP之间时,P(2,2)是该目标函数z=ax-y的唯一最优解,
所以a∈(-1,-
| 1 |
| 2 |
故选:D.
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若关于x的方程f(x)=|x-a|有三个不同的实根,则实数a的取值范围是( )
|
A、(-
| ||||
B、(0,
| ||||
C、(-
| ||||
D、(-
|
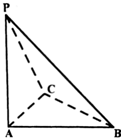 如图,在四面体P-ABC中,PA⊥平面ABC,△ABC是等腰直角三角形,且AC=BC=4,PA=4
如图,在四面体P-ABC中,PA⊥平面ABC,△ABC是等腰直角三角形,且AC=BC=4,PA=4