题目内容
已知抛物线y2=2x的焦点为F,与准线相切的圆C过点F并与抛物线相交于点M,若|MF|=
,则圆C的个数为( )
| 5 |
| 2 |
| A、8 | B、6 | C、4 | D、2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意,求出点M的坐标,讨论满足题意的圆C的圆心应在MF的中垂线与抛物线的交点上,求出满足条件的圆C多少即可.
解答:
解:设点M(x,y),
∵抛物线y2=2x的焦点是F(
,0),准线方程为x=-
,
∴|MF|=x-(-
)=
,
即x=2;
又点M在抛物线上,∴y2=4,解得y=±2,
∴M为(2,2)或(2,-2);
当M为(2,2)时,圆C与准线相切,且过点F与点M,圆心C应在MF的中垂线与抛物线的交点上,
此时交点有2个,∴圆C有2个;
同理,当M为(2,-2)时,圆C也有2个;
综上,满足条件的圆C有4个.
故选:C.
∵抛物线y2=2x的焦点是F(
| 1 |
| 2 |
| 1 |
| 2 |
∴|MF|=x-(-
| 1 |
| 2 |
| 5 |
| 2 |
即x=2;
又点M在抛物线上,∴y2=4,解得y=±2,
∴M为(2,2)或(2,-2);
当M为(2,2)时,圆C与准线相切,且过点F与点M,圆心C应在MF的中垂线与抛物线的交点上,
此时交点有2个,∴圆C有2个;
同理,当M为(2,-2)时,圆C也有2个;
综上,满足条件的圆C有4个.
故选:C.
点评:本题考查了抛物线的定义与几何性质的应用问题,解题的关键是求出点M的坐标,得出圆心C在MF的中垂线与抛物线的交点上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在极坐标系中,过点M(2,
)且垂直于OM(O为极点)的直线l的极坐标方程为( )
| π |
| 4 |
| A、ρ=2 | ||
| B、ρsinθ-ρcosθ=0 | ||
C、ρcos(θ+
| ||
D、ρcos(θ-
|
已知函数f(x)=
,若关于x的方程f(x)=|x-a|有三个不同的实根,则实数a的取值范围是( )
|
A、(-
| ||||
B、(0,
| ||||
C、(-
| ||||
D、(-
|
已知焦点在x轴上的椭圆的离心率为
,长轴长为8,则椭圆的标准方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
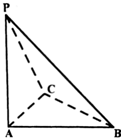 如图,在四面体P-ABC中,PA⊥平面ABC,△ABC是等腰直角三角形,且AC=BC=4,PA=4
如图,在四面体P-ABC中,PA⊥平面ABC,△ABC是等腰直角三角形,且AC=BC=4,PA=4 如图,在直角△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使得A1F⊥CD.
如图,在直角△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使得A1F⊥CD.