题目内容
已知等比数列{an}中，各项均为正数，且a6•a10+a3•a5=26，a5•a7=5，则a4+a8=（ ）
| A、4 | B、5 | C、6 | D、7 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质可知，a5•a7=a4•a8=5，a6•a10+a3•a5=26为a82+a42=26，再由题意和完全和平方公式求出a4+a8．
解答：
解：由等比数列的性质可知，a5•a7=a4•a8=5，
a6•a10+a3•a5=26，为a82+a42=26，
又各项均为正数，a4+a8=
=6，
故选：C．
a6•a10+a3•a5=26，为a82+a42=26，
又各项均为正数，a4+a8=
| a82+a42+2a4•a8 |
故选：C．
点评：本题考查了等比数列的性质的应用，以及利用完全和平方公式进行整体代换，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知1，a，b，c，4成等比数列，则实数b为（ ）
| A、4 | B、-2 | C、±2 | D、2 |
下列各图表示两个变量x、y的对应关系，则下列判断正确的是（ ）
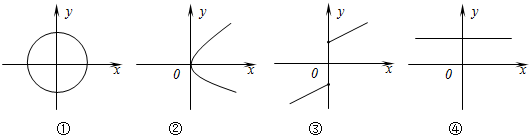
| A、都表示映射，都表示y是x的函数 |
| B、仅③表示y是x的函数 |
| C、仅④表示y是x的函数 |
| D、都不能表示y是x的函数 |
已知函数y=x2-2x-3的定义域为A，值域为B，则∁AB=（ ）
| A、[-4，+∞） |
| B、（-4，+∞） |
| C、R |
| D、（-∞，-4） |