题目内容
把数列(2n+1)按规律依次分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,则第104个括号内的各数之和为( )
| A、2036 | B、2048 |
| C、2060 | D、2072 |
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:由题意可知每四个括号一循环,里面共10个数,可得前103个括号中共有256个数,且第104个括号中有4个数515,517,519,521,由等差数列的求和公式可得.
解答:
解:由题意可知每四个括号一循环,里面共1+2+3+4=10个数,
∵103=4×25+3,∴前103个括号中共有数 25×10+1+2+3=256个数,
且第104个括号中有4个数,
∵2×257+1=515,
∴第104个括号内的数是515,517,519,521,
它们的和是
(515+521)×4=2072
故选:D
∵103=4×25+3,∴前103个括号中共有数 25×10+1+2+3=256个数,
且第104个括号中有4个数,
∵2×257+1=515,
∴第104个括号内的数是515,517,519,521,
它们的和是
| 1 |
| 2 |
故选:D
点评:本题考查等差数列的通项公式和求和公式,由题意总结出规律是解决问题的关键,属中档题.

练习册系列答案
相关题目
集合A={x∈Z|
<1},B={x∈N|lg(x-1)<
},从集合A,B中各取一个元素a,b,则a≠b的概率为( )
| 2x-1 |
| x-4 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}是公差不为0的等差数列,Sn是它的前n项和,a1,a3,a4成等比数列,若a2n=3Sn,则n=( )
| A、10 | B、12 | C、14 | D、16 |
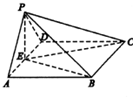 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.