题目内容
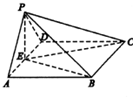 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.(1)试在线段AB上找一点F,使平面PCF⊥平面PBE,并说明理由;
(2)在(1)的条件下,求二面角E-PC-F的余弦值.
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)首先找出点FA所在的位置,进一步利用线面垂直的判定与性质的应用,面面垂直的判定,来说明结论成立.
(2)根据图形的特点建立空间直角坐标系,进一步求出平面的法向量,利用向量的夹角公式求出,二面角的余弦值.
(2)根据图形的特点建立空间直角坐标系,进一步求出平面的法向量,利用向量的夹角公式求出,二面角的余弦值.
解答:
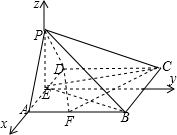 解:取点F为线段AB的中点,使得使平面PCF⊥平面PBE.
解:取点F为线段AB的中点,使得使平面PCF⊥平面PBE.
理由:在四棱锥P-ABCD中,E是线段AD的中点.
连接PE,平面PAD⊥平面ABCD,
所以:PE⊥平面ABCD.
做AB的中点F,在底面ABCD中,底面ABCD是正方形,△PAD是等边三角形,
所以:△ABE≌△BCF
则:∠ABE=∠BCF
所以:∠EBC+∠BCF=90°
则:BE⊥CF,
由于:PE⊥平面ABCD,
所以:PE⊥CF,
所以:CF⊥平面PBE
CF?平面PCF,
所以:平面PCF⊥平面PBE.
(2)建立空间直角坐标系E-xyz,设正方形ABCD的边长为2,则
得到:E(0,0,0),A(1,0,0),B(1,2,0),C(-1,2,0),F(1,1,0),P(0,0,
),
D(-1,0,0),
则:
=(2,-1,0),
=(1,1,-
),
连接DF,得到DF⊥平面PEC
所以:
可以看做是平面PEC的法向量.
=(2,1,0),
设平面PCF的法向量为
=(x,y,z)
则:
解得:
=(1,2,
)
所以:设二面角E-PC-F的平面角为θ
则:cosθ=
=
=
所以:二面角E-PC-F的余弦值为
.
 解:取点F为线段AB的中点,使得使平面PCF⊥平面PBE.
解:取点F为线段AB的中点,使得使平面PCF⊥平面PBE.理由:在四棱锥P-ABCD中,E是线段AD的中点.
连接PE,平面PAD⊥平面ABCD,
所以:PE⊥平面ABCD.
做AB的中点F,在底面ABCD中,底面ABCD是正方形,△PAD是等边三角形,
所以:△ABE≌△BCF
则:∠ABE=∠BCF
所以:∠EBC+∠BCF=90°
则:BE⊥CF,
由于:PE⊥平面ABCD,
所以:PE⊥CF,
所以:CF⊥平面PBE
CF?平面PCF,
所以:平面PCF⊥平面PBE.
(2)建立空间直角坐标系E-xyz,设正方形ABCD的边长为2,则
得到:E(0,0,0),A(1,0,0),B(1,2,0),C(-1,2,0),F(1,1,0),P(0,0,
| 3 |
D(-1,0,0),
则:
| CF |
| PF |
| 3 |
连接DF,得到DF⊥平面PEC
所以:
| DF |
| DF |
设平面PCF的法向量为
| n |
则:
|
解得:
| n |
| 3 |
所以:设二面角E-PC-F的平面角为θ
则:cosθ=
| ||||
|
|
| 4 | ||||
|
| ||
| 5 |
所以:二面角E-PC-F的余弦值为
| ||
| 5 |
点评:本题考查的知识要点:线面垂直的判定与性质的应用,面面垂直的判定,二面角的应用,法向量,空间直角坐标系的应用,向量的夹角公式的应用.

练习册系列答案
相关题目
 如图,⊙O的半径OC垂直于直径DB,F为BO上一点,CF的延长线交⊙O于点E,过E点的切线交DB的延长线于点A
如图,⊙O的半径OC垂直于直径DB,F为BO上一点,CF的延长线交⊙O于点E,过E点的切线交DB的延长线于点A 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=