题目内容
集合A={x∈Z|
＜1}，B={x∈N|lg（x-1）＜
}，从集合A，B中各取一个元素a，b，则a≠b的概率为（ ）
| 2x-1 |
| x-4 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：分别化简集合A，B，利用列举法求出A，B两个集合的元素，由古典概型公式解答．
解答：
解：集合A={x∈Z|
＜1}={x∈Z|-3＜x＜4}={-2，-1，0，1，2，3}，B={x∈N|lg（x-1）＜
}={x∈N|lg（x-1）＜
}={x∈N|1＜x＜
+1}={2，3，4}，
从集合A，B中各取一个元素a，b，有6×3=18种取法，使a≠b的取法有16种，从集合A，B中各取一个元素a，b，则a≠b的概率为故
=
；
故选：B．
| 2x-1 |
| x-4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
从集合A，B中各取一个元素a，b，有6×3=18种取法，使a≠b的取法有16种，从集合A，B中各取一个元素a，b，则a≠b的概率为故
| 16 |
| 18 |
| 8 |
| 9 |
故选：B．
点评：本题主要考查两个基本原理的应用，求随机事件的概率，属于基础题
练习册系列答案
轻松暑假总复习系列答案
相关题目
把数列（2n+1）按规律依次分为（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），（43），…，则第104个括号内的各数之和为（ ）
| A、2036 | B、2048 |
| C、2060 | D、2072 |
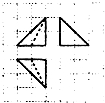如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|