题目内容
已知数列{an}是公差不为0的等差数列，Sn是它的前n项和，a1，a3，a4成等比数列，若a2n=3Sn，则n=（ ）
| A、10 | B、12 | C、14 | D、16 |
考点：等差数列与等比数列的综合
专题：等差数列与等比数列
分析：利用等比数列列出等差数列的首项与公差的关系，通过a2n=3Sn，得到方程，求解n即可．
解答：
解：数列{an}是公差不为0的等差数列，Sn是它的前n项和，a1，a3，a4成等比数列，
可得（a1+2d）2=a1（a1+3d），可得a1=-4d，
a2n=a1+（2n-1）d=a1-
（2n-1）a1，
3Sn=3（na1+
d）=3（na1-
a1）．
∵a2n=3Sn，
∴a1-
（2n-1）a1=3（na1-
a1）．
可得3n2-31n+10=0，
解得n=10．
故选：A．
可得（a1+2d）2=a1（a1+3d），可得a1=-4d，
a2n=a1+（2n-1）d=a1-
| 1 |
| 4 |
3Sn=3（na1+
| n(n-1) |
| 2 |
| n(n-1) |
| 8 |
∵a2n=3Sn，
∴a1-
| 1 |
| 4 |
| n(n-1) |
| 8 |
可得3n2-31n+10=0，
解得n=10．
故选：A．
点评：本题考查等差数列以及等比数列的应用，数列求和以及通项公式的求法，考查计算能力．
练习册系列答案
相关题目
把数列（2n+1）按规律依次分为（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），（43），…，则第104个括号内的各数之和为（ ）
| A、2036 | B、2048 |
| C、2060 | D、2072 |
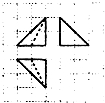如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|