题目内容
15．函数f（x）的图象与曲线y=x2-2x+3关于y轴对称，则f（x）=x2+2x+3．分析 若函数f（x）的图象与曲线y=x2-2x+3关于y轴对称，则f（x）=（-x）2-2（-x）+3，展开整理可得答案．
解答 解：若函数f（x）的图象与曲线y=x2-2x+3关于y轴对称，
则f（x）=（-x）2-2（-x）+3=x2+2x+3，
故答案为：x2+2x+3
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
5．“a=1”是“函数f（x）=a|x|+b，b∈R在区间[0，+∞）上为增函数”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
3．某同学在用描点法画二次函数y=ax2+bx+c的图象时，列出下面的表格：
由于粗心，他算错了其中一个y值，则这个错误的数值时（ ）
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A． | -11 | B． | -2 | C． | 1 | D． | -5 |
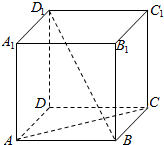已知正方体ABCD-A1B1C1D1的棱长是a，用向量法证明AC⊥BD1．
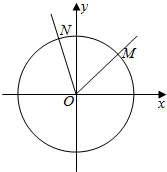如图，在直角坐标系xOy中，锐角α的顶点是原点，始边与x轴非负半轴重合，终边交单位圆于点M（x1，y1），将角α的终边按逆时针方向旋转$\frac{π}{3}$，交单位圆于点M（x2，y2）．记f（α）=y1+y2．