题目内容
在△ABC中,若角A,B,C满足sinAsinB+cosAsinB+cosBsinA+cosAcosB=2,则△ABC的形状一定是 .
考点:余弦定理
专题:解三角形
分析:已知等式左边利用两角和与差的正弦、余弦函数公式化简,根据正弦、余弦函数的值域确定出cos(A-B)与sin(A+B)的值都为1,利用特殊角的三角函数值求出A,B,C的度数,即可确定出三角形形状.
解答:
解:在△ABC中,sinAsinB+cosAsinB+cosBsinA+cosAcosB=2,
变形得:cos(A-B)+sin(A+B)=2,
∵-1≤cos(A-B)≤1,-1≤sin(A+B)≤1,
∴cos(A-B)=1且sin(A+B)=1,
∴A-B=0且A+B=
,即A=B=
,C=
,
则△ABC形状为等腰直角三角形.
故答案为:等腰直角三角形
变形得:cos(A-B)+sin(A+B)=2,
∵-1≤cos(A-B)≤1,-1≤sin(A+B)≤1,
∴cos(A-B)=1且sin(A+B)=1,
∴A-B=0且A+B=
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
则△ABC形状为等腰直角三角形.
故答案为:等腰直角三角形
点评:此题考查了两角和与差的正弦、余弦函数公式,特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
不等式2x2+2x-4≤
的解集为( )
| 1 |
| 2 |
| A、x≤-3或x≥-1 |
| B、-1≤x≤-3 |
| C、-3≤x≤1 |
| D、x≤-3或x≥1 |
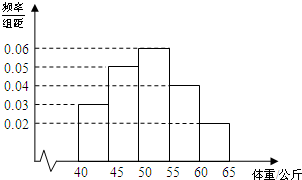 某校高三年级共1200人.学校为了检查同学们的健康状况,随机抽取了高三年级的100名同学作为样本,测量他们的体重(单位:公斤),体重的分组区间为[40,45),[45,50),[50,55),(55,60),[60,65],由此得到样本的频率分布直方图,如图.根据频率分布直方图,估计该校高三年级体重低于50公斤的人数为
某校高三年级共1200人.学校为了检查同学们的健康状况,随机抽取了高三年级的100名同学作为样本,测量他们的体重(单位:公斤),体重的分组区间为[40,45),[45,50),[50,55),(55,60),[60,65],由此得到样本的频率分布直方图,如图.根据频率分布直方图,估计该校高三年级体重低于50公斤的人数为