题目内容
20.将编号为1、2、3、4的四个小球随机的放入编号为1、2、3、4的四个纸箱中,每个纸箱有且只有一个小球,称此为一轮“放球”.设一轮“放球”后编号为i(i=1,2,3,4)的纸箱放入的 小球编号为ai,定义吻合度误差为X=|1-a1|+|2-a2|+|3-a3|+|4-a4|(1)写出吻合度误差X的可能值集合;
(2)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求吻合度误差X的分布列;
(3)某人连续进行了四轮“放球”,若都满足3<X<7,试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮“放球”相互独立).
分析 (1)根据题意知|1-a1|+|1-a3|与|1-a2|+|1-a4|的奇偶性相同,
误差X只能是偶数,由此写出X的可能取值;
(2)用列举法求出基本事件数,计算对应的概率值,写出随机变量X的分布列;
(3)利用互斥事件的概率公式计算对应的概率值.
解答 解:(1)由于在1、2、3、4中奇数与偶数各有两个,
所以a2、a4中的奇数的个数与a1、a3中偶数的个数相同;
因此,|1-a1|+|1-a3|与|1-a2|+|1-a4|的奇偶性相同,
从而吻合度误差X=|1-a1|+|2-a2|+|3-a3|+|4-a4|只能是偶数,
又因为X的值非负且值不大于8,
因此,吻合度误差X的可能值集合为{0,2,4,6,8};
(2)用(a1、a2、a3、a4)表示编号为1、2、3、4的四个纸箱中
放入的小球编号分别为a1、a2、a3、a4,则所有可能的结果如下:
(1,2,3,4),(1,2,4,3),(1,3,2,4),(1,3,4,2),(1,4,3,2),(1,4,2,3),
(2,1,3,4),(2,1,4,3),(2,3,1,4),(2,3,4,1),(2,4,3,1),(2,4,1,3),
(3,1,2,4),(3,1,4,2),(3,2,1,4),(3,2,4,1),(3,4,2,1),(3,4,1,2),
(4,1,2,3),(4,1,3,2),(4,2,1,3),(4,2,3,1),(4,3,1,2),(4,3,2,1),
计算P(X=0)=$\frac{1}{24}$,P(X=2)=$\frac{3}{24}$,P(X=4)=$\frac{7}{24}$,P(X=6)=$\frac{9}{24}$,P(X=8)=$\frac{4}{24}$;
于是,吻合度误差X的分布列如下:
| X | 0 | 2 | 4 | 6 | 8 |
| P | $\frac{1}{24}$ | $\frac{3}{24}$ | $\frac{7}{24}$ | $\frac{9}{24}$ | $\frac{4}{24}$ |
=$\frac{7}{24}$+$\frac{9}{24}$=$\frac{2}{3}$;
由上述结果和独立性假设,可得出现这种现象的概率为
P=${(\frac{2}{3})}^{4}$=$\frac{16}{81}$.
点评 本题考查了古典概型的概率以及离散型随机变量的分布列问题,是中档题.

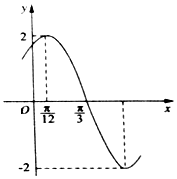 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)的图象关于点(-$\frac{11π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m∈(-2,-$\sqrt{3}$] | |
| D. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数 |
| A. | (0,π) | B. | $({0,\frac{π}{4}})$ | C. | $[{0,\frac{π}{4}})∪({\frac{3}{4}π,π})$ | D. | $[{0,\frac{π}{4}})∪({\frac{π}{2},π})$ |
| A. | -4 | B. | 16 | C. | -4或16 | D. | 16或18 |