题目内容
已知函数f(x)=ln(1+x)-kx(k∈R)
(Ⅰ)若f(x)最大值为0,求k的值;
(Ⅱ)已知数列{an}满足a1=1,an+1=ln(1+an)-
an;
(i)求证:
ai<2;(ii)是否存在n使得an∉(0,1],做不存在,请给予证明.
(Ⅰ)若f(x)最大值为0,求k的值;
(Ⅱ)已知数列{an}满足a1=1,an+1=ln(1+an)-
| 1 |
| 2 |
(i)求证:
| n |
 |
| i=1 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性,数列递推式
专题:计算题,证明题,函数的性质及应用,等差数列与等比数列
分析:(Ⅰ)求导f′(x)=
-k,x∈(-1,+∞),由导数讨论函数的单调性,从而求最值;
(Ⅱ)(i)由ln(x+1)≤x可推出an+1≤
an,从而可得an≤
an-1≤
an-2≤…≤
a1=
,进而可证明
ai<2;
(ii)用数学归纳法证明0<an≤1对任意正整数成立.
| 1 |
| 1+x |
(Ⅱ)(i)由ln(x+1)≤x可推出an+1≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| n |
 |
| i=1 |
(ii)用数学归纳法证明0<an≤1对任意正整数成立.
解答:
解:(Ⅰ)f′(x)=
-k,x∈(-1,+∞)
①当k≤0,无最值,舍去;
②k>0,fmax(x)=f(
-1)=0,
解得,k=1.
(Ⅱ)i.证明:由(Ⅰ)知,f(x)=ln(1+x)-x≤0,
即ln(x+1)≤x,
∴ln(1+an)≤an,
∴an+1=ln(1+an)-
an≤an-
an;
∴an+1≤
an,
∴an≤
an-1≤
an-2≤…≤
a1=
,
∴
ai=a1+a2+…+an≤1+
+(
)2+…+(
)n-1=2-21-n<2
ii.不存在,由(i)an≤(
)n-1<1,
下面用数学归纳法证明an>0对任意正整数成立,
①当n=1,a1=1>0;②假设当n=k时假设成立,即ak>0
令h(x)=ln(x+1)-
,
则h′(x)=
,
故h(x)在(-1,1)单调递增,
∵0<ak≤1,
∴ak+1=h(ak)>h(0)=0,
∴当n=k+1,an>0,
∴an>0,
∴对任意正整数an>0恒成立即不存在n∈N*,使an∉(0,1].
| 1 |
| 1+x |
①当k≤0,无最值,舍去;
②k>0,fmax(x)=f(
| 1 |
| k |
解得,k=1.
(Ⅱ)i.证明:由(Ⅰ)知,f(x)=ln(1+x)-x≤0,
即ln(x+1)≤x,
∴ln(1+an)≤an,
∴an+1=ln(1+an)-
| 1 |
| 2 |
| 1 |
| 2 |
∴an+1≤
| 1 |
| 2 |
∴an≤
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
∴
| n |
 |
| i=1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ii.不存在,由(i)an≤(
| 1 |
| 2 |
下面用数学归纳法证明an>0对任意正整数成立,
①当n=1,a1=1>0;②假设当n=k时假设成立,即ak>0
令h(x)=ln(x+1)-
| x |
| 2 |
则h′(x)=
| 1-x |
| 2(x+1) |
故h(x)在(-1,1)单调递增,
∵0<ak≤1,
∴ak+1=h(ak)>h(0)=0,
∴当n=k+1,an>0,
∴an>0,
∴对任意正整数an>0恒成立即不存在n∈N*,使an∉(0,1].
点评:本题主要考查导数研究函数最值、单调性、数列的递推公式、数列求和、放缩法证明不等式、数学归纳法等基础知识,考查推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想、特殊与一般思想及分类与整合思想.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
定义某种运算⊙:S=a⊙b的算原理如框图,则式子5⊙3+2⊙4=( )

| A、14 | B、15 | C、16 | D、18 |
命题p:幂函数y=x
在(-∞,0)上单调递减;命题q:已知函数f(x)=x3-3x2+m,若a,b,c∈[1,3],且f(a),f(b),f(c)能构成一个三角形的三边长,且4<m<8,则( )
| 2 |
| 3 |
| A、p且q为真命题 |
| B、p或q为假命题 |
| C、(¬p)且q为真命题 |
| D、p且(¬q)为真命题 |
已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=|
x0|,则x0=( )
| 5 |
| 4 |
| A、1 | B、2 | C、4 | D、8 |
一个几何体的三视图如图所示,则该几何体的底面积总和为( )
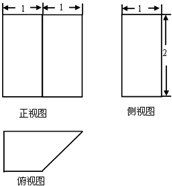

A、
| ||
| B、1 | ||
| C、3 | ||
| D、6 |