题目内容

5．若$5＜x＜6，P={（\frac{1}{2}）^x}，Q={log_2}x，R=\sqrt{x}$，则P，Q，R的大小关系是（　　）
A．Q＜P＜RB．P＜Q＜RC．Q＜R＜PD．P＜R＜Q

分析 5＜x＜6，可得P=$（\frac{1}{2}）^{x}$＜1．利用几何画板可得：y=log2x，y=$\sqrt{x}$的图象．可知：4＜x＜16时，2＜$\sqrt{x}$＜log2x．即可得出．

解答 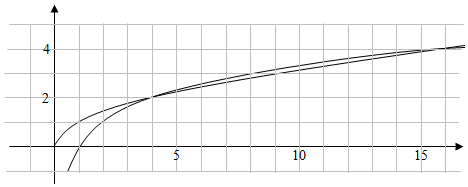解：∵5＜x＜6，
∵P=$（\frac{1}{2}）^{x}$＜1．
利用几何画板可得：y=log2x，y=$\sqrt{x}$的图象．
可知：当x=4时，$\sqrt{x}$=log2x=2．
当x=16时，$\sqrt{x}$=log2x=4．
当4＜x＜16时，
2＜$\sqrt{x}$＜log2x．
综上可得：P＜R＜Q．
故选：D．

点评 本题考查了指数函数与对数函数的单调性、利用几何画板比较函数值的大小关系，考查了数形结合方法、推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
20．数列{an}中，a1=-60，an+1=an+4．
（1）求通项an；
（2）求Sn=|a1|+|a2|+…+|an|．
16．已知抛物线C1：y2=2x与椭圆C2：$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1在第一象限交于点A，直线y=$\sqrt{2}$x+m与椭圆C2交于B、D两点，且A，B，D三点两两互不重合．
（1）求m的取值范围；
（2）△ABD的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由？
13．已知某物体的位移S（米）与时间t（秒）的关系是S（t）=3t-t2．
（Ⅰ）求t=0秒到t=2秒的平均速度；
（Ⅱ）求此物体在t=2秒的瞬时速度．
20．已知△ABC与△DBC都是边长为$\frac{{2\sqrt{3}}}{3}$的等边三角形，且平面ABC⊥平面DBC，过点A作PA⊥平面ABC，且AP=2．
（1）求直线PD与平面ABC所成角的大小；
（2）求二面角P-AD-C的余弦值；
（3）在线段PC上是否存在点E，使BE⊥平面ACD，并说明理由．
10．已知点A（2，2）和直线l：3x+4y-20=0．求：
（1）过点A和直线l平行的直线方程；
（2）过点A和直线l垂直的直线方程．
17．如图示，A，B分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点，F为其右焦点，2是|AF与|FB|的等差中项，$\sqrt{3}$是|AF|与|FB|的等比中项．点P是椭圆C上异于A、B的任一动点，过点A作直线l⊥x轴．以线段AF为直径的圆交直线AP于点A，M，连接FM交直线l于点Q．
（1）求椭圆C的方程；
（2）试问在x轴上是否存在一个定点N，使得直线PQ必过该定点N？若存在，求出N点的坐标，若不存在，说明理由．
14．函数y=|lnx|（0＜x≤e2）的值域是（　　）
A．（0，+∞）B．（0，2]C．[0，+∞）D．[2，+∞）
15．500辆汽车经过某一雷达地区，时速频率分布直方图如图所示，则时速超过60km/h的汽车数量为190辆．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网