题目内容
14.函数y=|lnx|(0<x≤e2)的值域是( )| A. | (0,+∞) | B. | (0,2] | C. | [0,+∞) | D. | [2,+∞) |
分析 由x的范围求出lnx的范围,取绝对值得答案.
解答 解:∵0<x≤e2,∴lnx≤2,
则|lnx|∈[0,+∞).
故选:C.
点评 本题考查函数值域的求法,考查了对数函数的性质,是基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
5.若$5<x<6,P={(\frac{1}{2})^x},Q={log_2}x,R=\sqrt{x}$,则P,Q,R的大小关系是( )
| A. | Q<P<R | B. | P<Q<R | C. | Q<R<P | D. | P<R<Q |
2.直线kx-y+k=0与圆(x-1)2+y2=1相切,则实数k等于( )
| A. | $\frac{1}{2}或-\frac{1}{2}$ | B. | $\frac{1}{3}或-\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}或-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}或-\frac{{\sqrt{2}}}{2}$ |
19.已知:$\left\{{\begin{array}{l}{2x+y-2≥0}\\{x+2y+4≥0}\\{3x-y-3≤0}\end{array}}\right.$,求z=x2+y2最小值为( )
| A. | 13 | B. | $\frac{4}{5}$ | C. | 1 | D. | $\frac{2}{3}$ |
6.若点P在抛物线y=x2上,点Q在圆x2+(y-4)2=1上,则|PQ|的最小值是( )
| A. | $\frac{{\sqrt{14}}}{2}-1$ | B. | $\frac{{\sqrt{15}}}{2}-1$ | C. | 2 | D. | $\sqrt{5}-1$ |
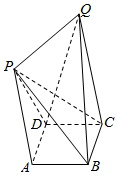 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.