题目内容
用20cm长的铁丝分成两段，每段各折成一个等边三角形，则这两个等边三角形面积和的最小值为 cm2．
考点：函数最值的应用
专题：函数的性质及应用
分析：设20cm长的铁丝分成两段长分别为x，20-x，易得两个等边三角形面积和S=
×(
)2×sin60°+
×(
)2×sin60°=
（x2-20x+200），由二次函数知识可得结论．
| 1 |
| 2 |
| x |
| 3 |
| 1 |
| 2 |
| 20-x |
| 3 |
| ||
| 18 |
解答：
解：设20cm长的铁丝分成两段长分别为x，20-x，
则每个正三角形的边长为
，
，0＜x＜20，
∴两个等边三角形面积和S=
×(
)2×sin60°+
×(
)2×sin60°，
=
[(
)2+(
)2]=
（x2-20x+200），
由二次函数知识可知当x=-
=10时，上式取最小值
故答案为：
则每个正三角形的边长为
| x |
| 3 |
| 20-x |
| 3 |
∴两个等边三角形面积和S=
| 1 |
| 2 |
| x |
| 3 |
| 1 |
| 2 |
| 20-x |
| 3 |
=
| ||
| 4 |
| x |
| 3 |
| 20-x |
| 3 |
| ||
| 18 |
由二次函数知识可知当x=-
| -20 |
| 2×1 |
50
| ||
| 9 |
故答案为：
50
| ||
| 9 |
点评：本题考查函数的最值的实际应用，构造函数并用二次函数的性质是解决问题的关键，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，向量
可以表示为①
-
；②
-
；③
+
；④
-
．（ ）
| BC |
| AB |
| AC |
| AC |
| AB |
| BA |
| AC |
| BA |
| CA |
| A、①②③ | B、①③④ |
| C、②③④ | D、①②④ |
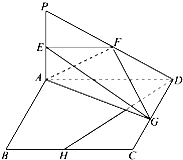如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且AD=2PA，E，F，G，H分别是线段PA，PD，CD，BC的中点．