题目内容
1.已知向量$\overrightarrow a=({1,1}),\overrightarrow b=({-1,0})$,若向量$k\overrightarrow a+\overrightarrow b$与向量$\overrightarrow c=({2,1})$共线,则实数k=-1.分析 根据向量的坐标运算和向量的共线定理即可求出
解答 解:∵向量$\overrightarrow a=({1,1}),\overrightarrow b=({-1,0})$,
∴向量$k\overrightarrow a+\overrightarrow b$=(k-1,k),
∵量$k\overrightarrow a+\overrightarrow b$与向量$\overrightarrow c=({2,1})$共线,
∴(k-1)×1=k×2,
解得k=-1,
故答案为:-1.
点评 本题考查了向量的坐标运算和向量的共线定理,属于基础题

练习册系列答案
相关题目
9.已知($\overline{z}$-1+3i)(2-i)=4+3i(其中i是虚数单位),则z的虚部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
16.在△ABC中,角A,B,C的对边分别为a,b,c,且bsinA+acos(B+C)=0,若$c=2,sinC=\frac{3}{5}$,则a+b等于( )
| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $2\sqrt{5}$ |
6.执行如图的程序框图,则输出x的值是( )
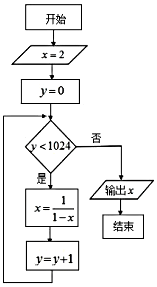

| A. | 2016 | B. | 1024 | C. | $\frac{1}{2}$ | D. | -1 |
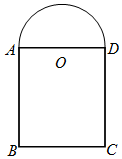 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).