题目内容
△ABC中,a=2,c=1,则∠C的取值范围是( )
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、(
|
考点:正弦定理
专题:解三角形
分析:由题意可得C为锐角,由正弦定理可得sinC=
sinA∈(0,
],可得C∈(0,
]
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
解答:
解:∵在△ABC中,a=2,c=1,
∴C为锐角(大边对大角),
∴由正弦定理可得
=
,
∴sinC=
sinA∈(0,
],
∴C∈(0,
]
故选:A
∴C为锐角(大边对大角),
∴由正弦定理可得
| 2 |
| sinA |
| 1 |
| sinC |
∴sinC=
| 1 |
| 2 |
| 1 |
| 2 |
∴C∈(0,
| π |
| 6 |
故选:A
点评:本题考查正弦定理,涉及三角函数的最值,属基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
方程
•
=|x+y-2|表示的曲线是( )
| 2 |
| (x+1)2+(y+1)2 |
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、不能确定 |
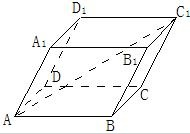 如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.
如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.