题目内容
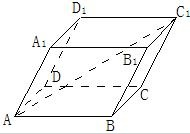如图，在平行六面体ABCD-A1B1C1D1中，AB=AD=AA1=1，∠BAD=60°，∠BAA1=∠DAA1=45°．（1）求BD1；
（2）求证：BD⊥面ACC1A1．
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）利用空间向量法即可求BD1；
（2）利用空间向量法证明
⊥
，
⊥
即可证明BD⊥面ACC1A1．
（2）利用空间向量法证明
| BD |
| AC |
| BD |
| AA1 |
解答：
解：（1）
=
-
=
+
-
，
|
|2=|
+
-
|=|
|2+|
|2+|
|2+2
•
-2
•
-2
•
|=1+1+1+2×1×1cos45°-2×1×1cos60°-2×1×1cos45°=3-1=2，
则|
|=
．
证明：（2）
=
-
，
=
+
，
则
•
=（
-
）•（
+
）=
2-
2=1-1=0，则
⊥
，即BD⊥AC，
•
=（
-
）•
=
•
-
•
=|
|•|
|cos45°-|
|•|
|cos45°=1×1×
-1×1×
=0，
故
⊥
，即BD⊥AA1，
∵AA1∩AC=A，
∴BD⊥面ACC1A1．
| BD1 |
| AD1 |
| AB |
| AD |
| AA1 |
| AB |
|
| BD1 |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AB |
则|
| BD1 |
| 2 |
证明：（2）
| BD |
| AD |
| AB |
| AC |
| AB |
| AD |
则
| BD |
| AC |
| AD |
| AB |
| AB |
| AD |
| AD |
| AB |
| BD |
| AC |
| BD |
| AA1 |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
| AB |
| AA1 |
| AD |
| AA1 |
| AB |
| AA1 |
| ||
| 2 |
| ||
| 2 |
故
| BD |
| AA1 |
∵AA1∩AC=A，
∴BD⊥面ACC1A1．
点评：本题主要考查空间向量的应用，利用空间向量的数量积求向量长度以及证明空间直线垂直．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
△ABC中，a=2，c=1，则∠C的取值范围是（ ）
A、（0，
| ||||
B、[
| ||||
C、[
| ||||
D、（
|
函数y=log
（3+2x-x2）的单调递增区间是（ ）
| 1 |
| 2 |
| A、（1，3） |
| B、（3，+∞） |
| C、（-∞，-1） |
| D、（-1，1） |
所有金属都能导电，铁是金属，所以铁能导电，属于哪种推理（ ）
| A、归纳推理 | B、类比推理 |
| C、合情推理 | D、演绎推理 |