题目内容
7.函数f(x)=ln$\frac{e+ex}{1-x}$的最大值为M,最小值为m,则M+m=( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 化简函数f(x)=1+ln$\frac{1+x}{1-x}$,设g(x)=ln$\frac{1+x}{1-x}$,则函数g(x)是定义域(-1,1)上的奇函数;由f(x)的最大值与最小值,得出g(x)的最大值与最小值,由此求出M+m的值.
解答 解:∵f(x)=ln$\frac{e+ex}{1-x}$=ln(e•$\frac{1+x}{1-x}$)=1+ln$\frac{1+x}{1-x}$,且$\frac{1+x}{1-x}$>0,∴-1<x<1;
设g(x)=ln$\frac{1+x}{1-x}$,则函数g(x)是定义域(-1,1)上的奇函数;
又f(x)的最大值为M,最小值为m,
∴g(x)的最大值是M-1,最小值是m-1;
∴(M-1)+(m-1)=0,
则M+m=2.
故选:C.
点评 本题考查了函数的奇偶性与最值的应用问题,是基础题目.

练习册系列答案
相关题目
15.惫设f(x)=-m(m+e)x2,g(x)=x2+(m-1)x-m,其中e均自然对数的底数,若?x∈R,使得f(x)<0或g(x)<0,则实数m的取值范围是( )
| A. | {m|-e≤m≤0} | B. | {m|0≤m≤e} | C. | {m∈R|m≠-1} | D. | {-1} |
16.sin17°sin223°-cos17°sin313°等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
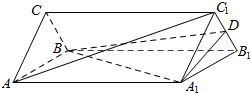 如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.
如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.