题目内容
18.用集合的语言表示下列语句,并画图表示:(1)平面α上有两点A、B,直线l过A、B;
(2)点A在直线l上,直线l与平面α无公共点;
(3)直线a与平面α相交于点P,直线b在平面α上且不经过点P.
分析 先准确理解文字叙述,再利用集合语言表示语句,然后作出图形.
解答 解:(1)∵平面α上有两点A、B,直线l过A、B,
∴用集合的语言表示为:
A∈α,B∈α,A∈l,B∈l,l?α.
画图表示为:
(2)∵点A在直线l上,直线l与平面α无公共点,
∴用集合的语言表示为:
A∈l,l∥α,
画图表示为:
(3)∵直线a与平面α相交于点P,直线b在平面α上且不经过点P,
∴用集合的语言表示为:
a∩α=P,b?α,P∉b,
画图表示为:
点评 本题考查平面的基本性质及推论的集合语言和图形表示,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
13.定义{x,y}max=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若a=tanθ,b=sinθ,c=cosθ,θ∈{θ|-$\frac{π}{4}$<θ<$\frac{3}{4}$π,θ≠0,$\frac{π}{4}$,$\frac{π}{2}$}且{a,b}max=a,{b,c}max=b,则θ的取值范围是( )
| A. | (-$\frac{π}{4}$,0) | B. | (0,$\frac{π}{4}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{2}$,$\frac{3}{4}$π) |
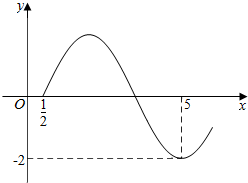 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.