题目内容
19.已知各项均为正数的数列{an}的前n项和为Sn,且对任意的n∈N+,恒有Sn2=a13+a23+…+an3.(1)求a1,a2的值;
(2)猜想数列{an}的通项公式an,并给予证明.
分析 (1)各项均为正数的数列{an}的前n项和为Sn,且对任意的n∈N+,恒有Sn2=a13+a23+…+an3.分别取n=1,2即可得出.
(2)猜想:an=n.利用数学归纳法证明即可得出.
解答 解:(1)∵各项均为正数的数列{an}的前n项和为Sn,且对任意的n∈N+,恒有Sn2=a13+a23+…+an3.
∴当n=1时,${a}_{1}^{2}$=${a}_{1}^{3}$,解得a1=1.
当n=2时,$(1+{a}_{2})^{2}$=1+${a}_{2}^{3}$,化为:${a}_{2}^{2}$-a2-2=0,解得a2=2.
(2)猜想:an=n.
下面利用数学归纳法证明:①当n=1时,a1=1成立.
②假设当n=k∈N*时,ak=k.
则当n=k+1时,${S}_{k+1}^{2}$-${S}_{k}^{2}$=${a}_{k+1}^{3}$,
∴Sk+1+Sk=${a}_{k+1}^{2}$,
∴${a}_{k+1}^{2}$-ak+1-2Sk=0,
即${a}_{k+1}^{2}$-ak+1-2×$\frac{k(k+1)}{2}$=0,
解得ak+1=k+1.
因此当n=k+1时也成立,
综上可得:?n∈N*an=n成立.
点评 本题考查了递推关系的应用、数学归纳法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.空间四点中,无三点共线是四点共面的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要 |
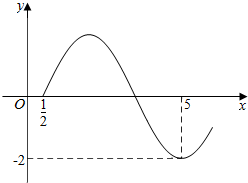 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.