题目内容

15．设f（x）=$\left\{\begin{array}{l}{1+lo{g}_{2}（2-x），（x＜1）}\\{{2}^{x-1}，（x≥1）}\end{array}\right.$，则f（-6）+f（log212）的值为（　　）
A．8B．9C．10D．12

分析 由已知得f（-6）=1+log28=4，f（log212）=${2}^{lo{g}_{2}12}$÷2=6，由此能求出f（-6）+f（log212）．

解答 解：∵f（x）=$\left\{\begin{array}{l}{1+lo{g}_{2}（2-x），（x＜1）}\\{{2}^{x-1}，（x≥1）}\end{array}\right.$，
∴f（-6）=1+log28=4，
f（log212）=${2}^{lo{g}_{2}12}$÷2=6，
∴f（-6）+f（log212）=4+6=10．
故选：C．

点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案
相关题目
5．设点P（x，y）是曲线a|x|+b|y|=1（a＞0，b＞0）上任意一点，其坐标（x，y）也满足$\sqrt{{x}^{2}+{y}^{2}+2x+1}$+$\sqrt{{x}^{2}+{y}^{2}-2x+1}$≤2$\sqrt{2}$，则$\sqrt{2}$a+b取值范围为（　　）
A．（0，2]B．[1，2]C．[1，+∞）D．[2，+∞）
6．已知圆C1：x2+y2=4与圆C2：（x-1）2+（y-3）2=4，过动点P（a，b）分别作圆C1、圆C2的切线PM，PN，（M，N分别为切点），若|PM|=|PN|，则a2+b2-6a-4b+13的最小值是（　　）
A．5B．$\frac{8}{5}$C．$\frac{2}{5}\sqrt{10}$D．$\frac{1}{3}$
3．函数y=f（x）导函数f'（x）的图象如图所示，则下列说法正确的是（　　）
A．函数y=f（x）在（-∞，0）上单调递增B．函数y=f（x）的递减区间为（3，5）
C．函数y=f（x）在x=0处取得极大值D．函数y=f（x）在x=5处取得极小值
10．已知椭圆C的两焦点分别为F1（-2$\sqrt{2}$，0）、F2（2$\sqrt{2}$，0），长轴长为6．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知过点（0，2）且斜率为1的直线交椭圆C于A，B两点，试探究原点O是否在以线段AB为直径的圆上．
20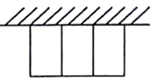．有一批材料可以建成80m的围墙，若用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的小矩形（如图所示），且围墙厚度不计，则围成的矩形的最大面积为（　　）
A．200m2B．360m2C．400m2D．480m2
7．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象与y轴的交点为（0，$\sqrt{3}$），它的一个对称中心是M（$\frac{π}{3}$，0），点M与最近的一条对称轴的距离是$\frac{π}{4}$．
（1）求此函数的解析式；
（2）求此函数取得最大值时x的取值集合；
（3）当x∈（0，π）时，求此函数的单调递增区间．
4．在等比数列{an}中，已知a7•a19=8，则a3•a23=（　　）
A．6B．7C．8D．9
12．已知函数f（x）=sin（2x+$\frac{π}{3}$），对任意的x1，x2，x3，且0≤x1＜x2＜x3≤π，都有|f（x1）-f（x2）|+|f（x2）-f（x3）|≤m成立，则实数m的最小值为3+$\frac{\sqrt{3}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网