题目内容
求过点（-3，3）且被圆x2+y2+4y-21=0所截得的弦长为8的直线方程．
考点：直线与圆相交的性质
专题：直线与圆
分析：把圆的方程化为标准方程，可得圆心坐标与圆的半径，根据直线与圆的相交弦长为8求得圆心到直线的距离，再利用点到直线的距离公式确定直线的斜率，再验证斜率不存在时是否符合．
解答：
解：圆的标准方程为：x2+（y+2）2=25，
∴圆的圆心为（0，-2），半径为R=5，
设过点（-3，3）的直线方程为y-3=k（x+3）或x=-3，
∵弦长为8，∴圆心到直线的距离d=
=3，
∴
=3⇒k=-
，
又x=-3时，圆心到直线的距离也为3，
∴符合条件的直线有8x+15y-21=0或x+3=0．
∴圆的圆心为（0，-2），半径为R=5，
设过点（-3，3）的直线方程为y-3=k（x+3）或x=-3，
∵弦长为8，∴圆心到直线的距离d=
| 52-42 |
∴
| |2+3k+3| | ||
|
| 8 |
| 15 |
又x=-3时，圆心到直线的距离也为3，
∴符合条件的直线有8x+15y-21=0或x+3=0．
点评：本题考查了直线与圆的相交弦长问题及点到直线的距离公式，直线与圆的相交弦长为2
，（其中R为圆的半径，d为圆心到直线的距离）．
| R2-d2 |
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
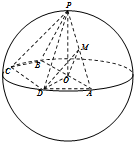如图，平面四边形ABCD的四个顶点都在球O的表面上，AB为球O的直径，P为球面上一点，且PO⊥平面ABCD，NC=CD=DA=2，点M为PA的中点．