题目内容
边长为2的正三角形ABC中,D,E,M分别是AB,AC,BC的中点,N为DE的中点,将△ADE沿DE折起至A′DE位置,使A′M=
,设MC的中点为Q,A′B的中点为P,则
①A′N⊥平面BCED
②NQ∥平面A′EC
③DE⊥平面A′MN
④平面PMN∥平面A′EC
以上结论正确的是( )
| ||
| 2 |
①A′N⊥平面BCED
②NQ∥平面A′EC
③DE⊥平面A′MN
④平面PMN∥平面A′EC
以上结论正确的是( )
| A、①②④ | B、②③④ |
| C、①②③ | D、①③④ |
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:①由等边三角形的性质可得A′N=AN=MN=
,可得A′N2+MN2=(
)2×2=A′M2.可得A′N⊥MN,又A′N⊥DE,利用线面垂直的判定定理即可得出.
②由于NQ∥AC,利用线面平行的判定定理可得NQ∥平面A′EC;
③由①可得A′N⊥平面BCED,A′N⊥DE,又DE⊥MN,利用线面垂直的判定定理即可得出;
④由于MN∩平面A′EC=A,因此平面PMN∥平面A′EC不正确.
| ||
| 2 |
| ||
| 2 |
②由于NQ∥AC,利用线面平行的判定定理可得NQ∥平面A′EC;
③由①可得A′N⊥平面BCED,A′N⊥DE,又DE⊥MN,利用线面垂直的判定定理即可得出;
④由于MN∩平面A′EC=A,因此平面PMN∥平面A′EC不正确.
解答:
解:如图所示,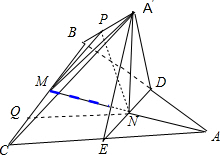
①由等边三角形的性质可得A′N=AN=MN=
,∴A′N2+MN2=(
)2×2=A′M2.∴A′N⊥MN,
又A′N⊥DE,ED∩MN=N,∴A′N⊥平面BCED,正确.
②∵NQ∥AC,NQ?平面A′EC,AC?平面A′EC,∴NQ∥平面A′EC,正确;
③由①可得A′N⊥平面BCED,∴A′N⊥DE,又DE⊥MN,MN∩A′N=N,∴DE⊥平面A′MN,正确;
④∵MN∩平面A′EC=A,∴平面PMN∥平面A′EC不正确.
综上可得:只有①②③正确.
故选:C.

①由等边三角形的性质可得A′N=AN=MN=
| ||
| 2 |
| ||
| 2 |
又A′N⊥DE,ED∩MN=N,∴A′N⊥平面BCED,正确.
②∵NQ∥AC,NQ?平面A′EC,AC?平面A′EC,∴NQ∥平面A′EC,正确;
③由①可得A′N⊥平面BCED,∴A′N⊥DE,又DE⊥MN,MN∩A′N=N,∴DE⊥平面A′MN,正确;
④∵MN∩平面A′EC=A,∴平面PMN∥平面A′EC不正确.
综上可得:只有①②③正确.
故选:C.
点评:本题综合考查了线面面面平行与垂直的判定性质定理、三角形的中位线定理、勾股定理的逆定理,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知全集U={0,1,2,3,4,5,6},集合A={2,4,5},B={1,3,4,6},则(∁uA)∩B为( )
| A、{0,1,3,6} |
| B、{0,2,4,6} |
| C、{0,1,6} |
| D、{1,3,6} |
已知θ为第二象限角,sinθ,cosθ是关于x的方程2x2+(
-1)x+m=0(m∈R)的两根,则sinθ-cosθ的等于( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
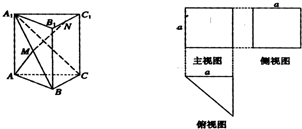 一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点.
一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点. 如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2
如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2