题目内容
 四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=
四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=| π |
| 3 |
(1)求证:EF∥面PCD;
(2)求证:AD⊥PB;
(3)求三棱锥C-BDP的体积.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)取PD中点为G,连接GC、GF∵FG
EC,∴四边形CEFG为平行四边形,利用线面平行的判定定理可得所求;
(2)取AD中点为H,连接PH,BH,△PAD中,PA=PD,H为AD中点⇒PH⊥AD,由等边三角形得到AD⊥BH,得到AD⊥面PBH,再由平面垂直的性质解答;
(3)求出三棱锥C-BDP的高PH,利用三棱锥的体积解答.
| ||
. |
(2)取AD中点为H,连接PH,BH,△PAD中,PA=PD,H为AD中点⇒PH⊥AD,由等边三角形得到AD⊥BH,得到AD⊥面PBH,再由平面垂直的性质解答;
(3)求出三棱锥C-BDP的高PH,利用三棱锥的体积解答.
解答:
解:(1)取PD中点为G,连接GC、GF∵FG
EC,∴四边形CEFG为平行四边形,
故
⇒EF∥面PCD,
(2)取AD中点为H,连接PH,BH△PAD中,PA=PD,H为AD中点⇒PH⊥AD,
正△ABD中,H为AD中点⇒BH⊥AD,
故AD⊥面PBH⇒AD⊥PB.
(3)
⇒PH⊥面ABCD,且PH=3,
所以VC-BDP=VP-BCD=
S△BCD•PH=
×(
×8×8×sin
)×3=16
.
| ||
. |
故
|
(2)取AD中点为H,连接PH,BH△PAD中,PA=PD,H为AD中点⇒PH⊥AD,
正△ABD中,H为AD中点⇒BH⊥AD,
故AD⊥面PBH⇒AD⊥PB.
(3)
|
所以VC-BDP=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |
点评:本题考查了线面平行和线面垂直的性质以及判定定理 的运用,考查三棱锥体积的求法,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
函数y=
+x的图象可能是( )
| |x| |
| x |
A、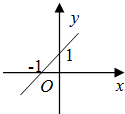 |
B、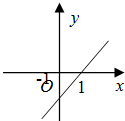 |
C、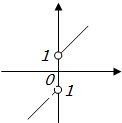 |
D、 |
某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|