题目内容
16．若f（x）=$\left\{\begin{array}{l}{{e}^{x-2}，x≤2}\\{ln（x-1），x＞2}\end{array}\right.$，则f[f（4）]=$\frac{3}{{e}^{2}}$．分析 根据分段函数的表达式，利用代入法进行求解即可．
解答 解：由分段函数的表达式得f（4）=ln3＜2，
则f（ln3）=eln3-2=$\frac{{e}^{ln3}}{{e}^{2}}$=$\frac{3}{{e}^{2}}$，
故f[f（4）]=$\frac{3}{{e}^{2}}$，
故答案为：$\frac{3}{{e}^{2}}$．
点评 本题主要考查函数值的计算，根据分段函数的表达式利用代入法是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
8．海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如图：
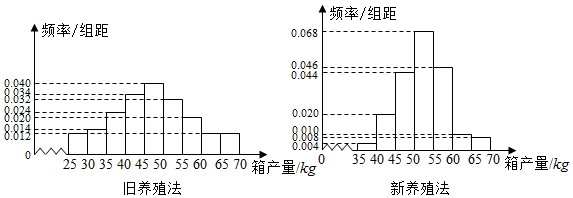
（1）设两种养殖方法的箱产量相互独立，记A表示事件“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）．
附：
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
（1）设两种养殖方法的箱产量相互独立，记A表示事件“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
| 箱产量＜50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
附：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
9．设集合A={1，2，6}，B={2，4}，C={1，2，3，4}，则（A∪B）∩C=（ ）
| A． | {2} | B． | {1，2，4} | C． | {1，2，4，6} | D． | {1，2，3，4，6} |
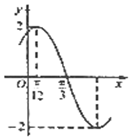已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，下列说法正确的有（ ）个