题目内容
已知函数f(x)、g(x)的定义域都是R′∪R″,J(x)=f(x)•g(x).
(1)如果f(x),g(x)都是奇函数,试推出函数J(x)的奇偶性,并予以证明;若f(x),g(x)都是偶函数,或一个是奇函数另一个是偶函数,则请分别写出关于函数J(x)的奇偶性的相应结论;
(2)若函数f(x)为奇函数,g(x)为非奇非偶函数,试用反证法证明函数J(x)为非奇非偶函数;若函数f(x)为偶函数,g(x)为非奇非偶函数,则请分别写出关于函数J(x)的奇偶性的相应结论;
(3)若f(x),g(x)都是非奇非偶函数,则函数J(x)的奇偶性能否确定?请写出相应的结论并证明;若不能,请分别举例说明各种可能的情况.
(1)如果f(x),g(x)都是奇函数,试推出函数J(x)的奇偶性,并予以证明;若f(x),g(x)都是偶函数,或一个是奇函数另一个是偶函数,则请分别写出关于函数J(x)的奇偶性的相应结论;
(2)若函数f(x)为奇函数,g(x)为非奇非偶函数,试用反证法证明函数J(x)为非奇非偶函数;若函数f(x)为偶函数,g(x)为非奇非偶函数,则请分别写出关于函数J(x)的奇偶性的相应结论;
(3)若f(x),g(x)都是非奇非偶函数,则函数J(x)的奇偶性能否确定?请写出相应的结论并证明;若不能,请分别举例说明各种可能的情况.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用函数奇偶性的定义即可判断出.
解答:
解:(1)J(x)是偶函数.证明如下:
J(-x)=f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)•g(x)=J(x),
∴J(x)是偶函数.
若f(x),g(x)都是偶函数,则J(x)是偶函数.
若一个是奇函数另一个是偶函数,函数J(x)是奇函数.
(2)函数f(x)为奇函数,g(x)为非奇非偶函数,则函数J(x)为非奇非偶函数.
反证法证明:假设函数J(x)是奇函数,则f(-x)g(-x)=-f(x)g(-x)=-f(x)g(x),
∴g(-x)=g(x)为偶函数,与g(x)为非奇非偶函数矛盾,因此假设不成立.
若函数f(x)为偶函数,g(x)为非奇非偶函数,则函数J(x)是非奇非偶函数.
(3)若f(x),g(x)都是非奇非偶函数,则函数J(x)的奇偶性不能确定.
①取f(x)=ex,g(x)=e-x,则J(x)=1既是奇函数又是偶函数;
②取f(x)=x+1,g(x)=x-1,则J(x)=x2-1为偶函数.
③取f(x)=
,g(x)=
,假设定义域为(-∞,-1)∪(1,+∞),则J(x)是奇函数.
④取f(x)=e2x,g(x)=e-x,则J(x)=ex是非奇非偶函数.
J(-x)=f(-x)•g(-x)=-f(x)•[-g(x)]=f(x)•g(x)=J(x),
∴J(x)是偶函数.
若f(x),g(x)都是偶函数,则J(x)是偶函数.
若一个是奇函数另一个是偶函数,函数J(x)是奇函数.
(2)函数f(x)为奇函数,g(x)为非奇非偶函数,则函数J(x)为非奇非偶函数.
反证法证明:假设函数J(x)是奇函数,则f(-x)g(-x)=-f(x)g(-x)=-f(x)g(x),
∴g(-x)=g(x)为偶函数,与g(x)为非奇非偶函数矛盾,因此假设不成立.
若函数f(x)为偶函数,g(x)为非奇非偶函数,则函数J(x)是非奇非偶函数.
(3)若f(x),g(x)都是非奇非偶函数,则函数J(x)的奇偶性不能确定.
①取f(x)=ex,g(x)=e-x,则J(x)=1既是奇函数又是偶函数;
②取f(x)=x+1,g(x)=x-1,则J(x)=x2-1为偶函数.
③取f(x)=
| x+1 |
| x |
| x2 |
| x+1 |
④取f(x)=e2x,g(x)=e-x,则J(x)=ex是非奇非偶函数.
点评:本题考查了函数的奇偶性定义及其判定方法,考查了推理能力与举例能力,属于难题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
在下列四个命题中,其中正确命题的是( )
| A、有两个面互相平行,其余各面都是平行四边形的多面体是棱柱 |
| B、有一个面是多边形,其余各面都是三角形的几何体叫棱锥 |
| C、有两个面互相平行,其余各面都是梯形的多面体是棱台 |
| D、用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 |
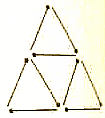 用9根火柴棒搭成的图案如图所示,移动2根火柴棒,使这9根火柴棒搭成一个中心对称图形,并画出这个图形.
用9根火柴棒搭成的图案如图所示,移动2根火柴棒,使这9根火柴棒搭成一个中心对称图形,并画出这个图形.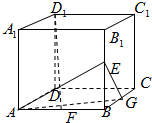 如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.
如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点. 一个三棱柱的底面是正三角形,侧面垂直于底面,它的三视图及其尺寸如图(单位:cm).则该三棱柱的表面积为
一个三棱柱的底面是正三角形,侧面垂直于底面,它的三视图及其尺寸如图(单位:cm).则该三棱柱的表面积为