题目内容
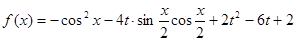
(
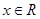 ),其中
),其中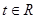 ,将
,将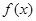 的最小值记为
的最小值记为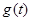 ,
,(1)求
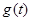 的表达式;
的表达式;(2)当
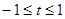 时,要使关于
时,要使关于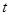 的方程
的方程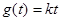 有且仅有一个实根,求实数
有且仅有一个实根,求实数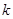 的取值范围.
的取值范围.(1) ;(2)
;(2)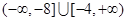 .
.
 ;(2)
;(2)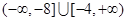 .
. (1)先化简f(x),则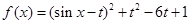 ,然后根据二次函数的性质讨论t的范围,进而确定
,然后根据二次函数的性质讨论t的范围,进而确定 .
.
(2) 当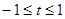 时,
时,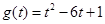 ,方程
,方程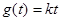 即:
即:
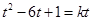 即方程
即方程 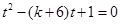 在区间
在区间 有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.
有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.
解:(1)由已知有: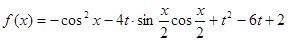
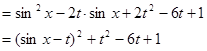
由于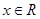 ,∴
,∴ 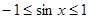 ………………………3分
………………………3分
∴ 当 时,则当
时,则当 时,
时,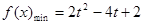 ;
;
当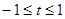 时,则当
时,则当 时,
时,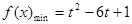 ;
;
当 时,则当
时,则当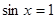 时,
时,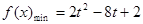 ;
;
综上, …………………7分
…………………7分
(2)当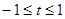 时,
时,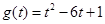 ,方程
,方程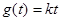 即:
即:
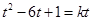 即方程
即方程 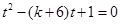 在区间
在区间 有且仅有一个实根,8分
有且仅有一个实根,8分
令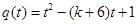 ,则有:
,则有:
解法1:①若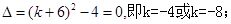
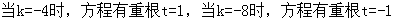
∴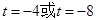 ……10分
……10分
②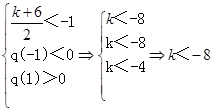 或
或 
综上,当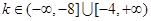 时,关于
时,关于 的方程
的方程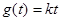 在区间
在区间 有且仅
有且仅
有一个实根. ……………………………………14分
解法2:由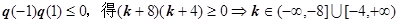 .
.
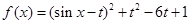 ,然后根据二次函数的性质讨论t的范围,进而确定
,然后根据二次函数的性质讨论t的范围,进而确定 .
.(2) 当
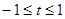 时,
时,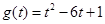 ,方程
,方程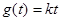 即:
即: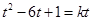 即方程
即方程 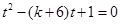 在区间
在区间 有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.
有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.解:(1)由已知有:
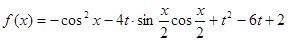
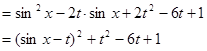
由于
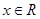 ,∴
,∴ 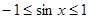 ………………………3分
………………………3分∴ 当
 时,则当
时,则当 时,
时,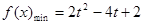 ;
;当
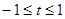 时,则当
时,则当 时,
时,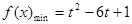 ;
;当
 时,则当
时,则当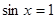 时,
时,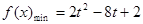 ;
;综上,
 …………………7分
…………………7分(2)当
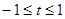 时,
时,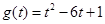 ,方程
,方程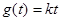 即:
即: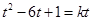 即方程
即方程 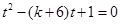 在区间
在区间 有且仅有一个实根,8分
有且仅有一个实根,8分令
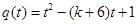 ,则有:
,则有:解法1:①若
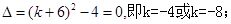
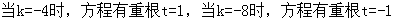
∴
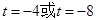 ……10分
……10分②
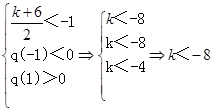 或
或 
综上,当
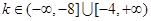 时,关于
时,关于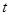 的方程
的方程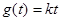 在区间
在区间 有且仅
有且仅有一个实根. ……………………………………14分
解法2:由
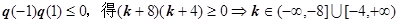 .
.
练习册系列答案
相关题目
 .
. ,求使
,求使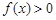 时
时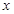 的取值范围;
的取值范围;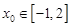 使
使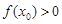 成立,求实数
成立,求实数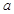 的取值范围.
的取值范围.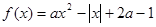 (
(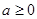 )
)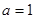 ,作出函数
,作出函数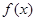 的图象;
的图象;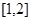 上的最小值为
上的最小值为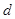 ,求
,求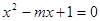 的两个根为
的两个根为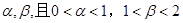 ,则实数m的
,则实数m的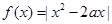
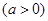 ,
,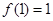 时, 求
时, 求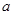 的值;
的值;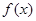 在
在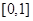 上的最大值为
上的最大值为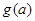
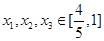 ,以
,以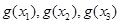 的值为边长的三条线段是否可构成三角形?请说明理由。
的值为边长的三条线段是否可构成三角形?请说明理由。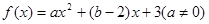 ,
,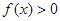 的解集
的解集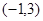 .求
.求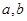 的值;
的值;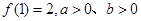 求
求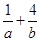 的最小值.
的最小值.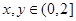 ,且
,且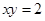 ,且
,且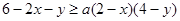 恒成立,则实数
恒成立,则实数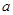 取值范围是
取值范围是 
 .
. ,都有
,都有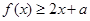 ,求
,求 的取值范围;
的取值范围; 时,
时,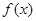 的最大值为M,求证:
的最大值为M,求证: ;
; ,求证:对于任意的
,求证:对于任意的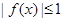 的充要条件是
的充要条件是