题目内容
设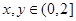 ,且
,且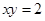 ,且
,且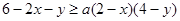 恒成立,则实数
恒成立,则实数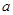 取值范围是
取值范围是
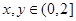 ,且
,且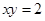 ,且
,且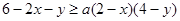 恒成立,则实数
恒成立,则实数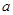 取值范围是
取值范围是 
解:因为设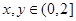 ,且
,且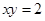 ,且
,且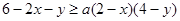 恒成立
恒成立
转化为 ,利用函数的性质可以求解得到最小值为1.
,利用函数的性质可以求解得到最小值为1.
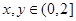 ,且
,且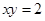 ,且
,且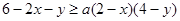 恒成立
恒成立转化为
 ,利用函数的性质可以求解得到最小值为1.
,利用函数的性质可以求解得到最小值为1.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
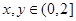 ,且
,且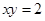 ,且
,且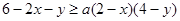 恒成立,则实数
恒成立,则实数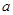 取值范围是
取值范围是 
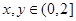 ,且
,且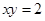 ,且
,且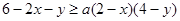 恒成立
恒成立 ,利用函数的性质可以求解得到最小值为1.
,利用函数的性质可以求解得到最小值为1.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案