题目内容
已知函数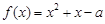 .
.
(1) 若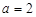 ,求使
,求使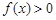 时
时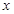 的取值范围;
的取值范围;
(2) 若存在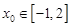 使
使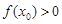 成立,求实数
成立,求实数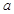 的取值范围.
的取值范围.
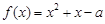 .
.(1) 若
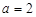 ,求使
,求使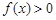 时
时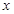 的取值范围;
的取值范围;(2) 若存在
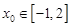 使
使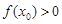 成立,求实数
成立,求实数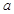 的取值范围.
的取值范围.(1)  或
或 (2)
(2) 
 或
或 (2)
(2) 
本试题主要是考查了函数与不等式综合运用。
(1)因为若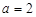 ,求使
,求使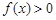 ,解
,解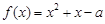 >0,得到
>0,得到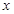 的取值范围为
的取值范围为 或
或 -
-
(2)由题应有 即可,利用二次函数的性质可得。
即可,利用二次函数的性质可得。
解:(I)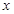 的取值范围为
的取值范围为 或
或 --------(6分)
--------(6分)
(II)由题应有 --------------(9分)
--------------(9分)
而 ,当
,当 时
时 , --------(11分)
, --------(11分)
所以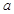 的取值范围为
的取值范围为 ----------(12分)
----------(12分)
(1)因为若
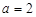 ,求使
,求使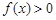 ,解
,解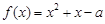 >0,得到
>0,得到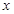 的取值范围为
的取值范围为 或
或 -
-(2)由题应有
 即可,利用二次函数的性质可得。
即可,利用二次函数的性质可得。解:(I)
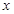 的取值范围为
的取值范围为 或
或 --------(6分)
--------(6分)(II)由题应有
 --------------(9分)
--------------(9分)而
 ,当
,当 时
时 , --------(11分)
, --------(11分)所以
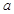 的取值范围为
的取值范围为 ----------(12分)
----------(12分)
练习册系列答案
相关题目
 ,设函数
,设函数 ,
, ,且函数
,且函数 的值域为
的值域为 ,求
,求 在
在 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.
 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.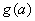 的函数表达式;
的函数表达式; x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,
x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,  )点
)点 .
. 在闭区间
在闭区间 上的大致图像;
上的大致图像; 与
与 的取值范围.
的取值范围. 是不共线的两向量,其夹角是
是不共线的两向量,其夹角是 ,若函数
,若函数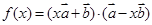 (
( )在
)在 上有最大值,则( )
上有最大值,则( ) ,且
,且 ,且
,且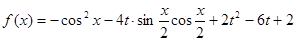
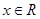 ),其中
),其中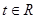 ,将
,将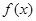 的最小值记为
的最小值记为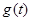 ,
,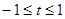 时,要使关于
时,要使关于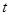 的方程
的方程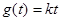 有且仅有一个实根,求实数
有且仅有一个实根,求实数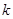 的取值范围.
的取值范围. 且
且 ,则
,则 的最小值是______
的最小值是______  的单调增区间为_________________。
的单调增区间为_________________。