题目内容
18.某工厂今年年初贷款a万元,年利率为r(按复利计算),从今年末起,每年年末偿还固定数量金额,5年内还清,则每年应还金额为( )万元.| A. | $\frac{{{{({1+r})}^5}a}}{{{{({1+r})}^5}-1}}$ | B. | $\frac{{{{({1+r})}^5}ar}}{{{{({1+r})}^5}-1}}$ | C. | $\frac{{{{({1+r})}^5}ar}}{{{{({1+r})}^5}+1}}$ | D. | $\frac{ra}{{{{({1+r})}^5}}}$ |
分析 假设每年偿还x元,由题意可得a(1+r)5=x(1+r)4+x(1+r)3+…+x(1+r)+x,利用等比数列的前n项和公式即可得出.
解答 解:假设每年偿还x元,由题意可得a(1+r)5=x(1+r)4+x(1+r)3+…+x(1+r)+x,
化为a(1+r)5=x•$\frac{(1+r)^{5}-1}{(1+t)-1}$,解得x=$\frac{ar(1+r)^{5}}{(1+r)^{5}-1}$.
故选:B.
点评 本题考查了等比数列的前n项和公式的应用,属于中档题.

练习册系列答案
相关题目
9.直线2x-y+4=0同时过第( )象限.
| A. | 一,二,三 | B. | 二,三,四 | C. | 一,二,四 | D. | 一,三,四 |
6.根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,若$\stackrel{∧}{a}$=4.5,则x每增加1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加0.9个单位 | B. | 减少0.9个单位 | C. | 增加0.72个单位 | D. | 减少0.72个单位 |
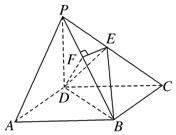 如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.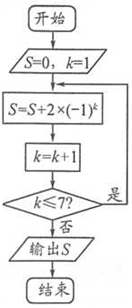 已知某算法的程序框图如图所示,则输出的S的值是-2.
已知某算法的程序框图如图所示,则输出的S的值是-2. 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )