题目内容
若等比数列{an}的前n项和Sn=2•3n+a(a为常数),则a= .
考点:等比数列的前n项和
专题:计算题,等差数列与等比数列
分析:由Sn=2•3n+a,以及n≥2时,an=Sn-Sn-1,可分别求出数列{an}的前三项,再根据列{an}是等比数列,即可求出常数k的值.
解答:
解:因为数列{an}的前n项和Sn=2•3n+a,所以S1=6+a,S2=18+a,S3=54+a,
又因为a1=S1,a2=S2-S1,a3=S3-S2,所以a1=6+a,a2=12,a3=36,
根据数列{an}是等比数列,可知a1a3=a22,所以(6+a)×36=122,解得a=-2.
故答案为:-2.
又因为a1=S1,a2=S2-S1,a3=S3-S2,所以a1=6+a,a2=12,a3=36,
根据数列{an}是等比数列,可知a1a3=a22,所以(6+a)×36=122,解得a=-2.
故答案为:-2.
点评:本题考查了等比数列的其前n项和Sn与通项an的关系,属基础题,应该掌握.

练习册系列答案
相关题目
已知向量
=(2,1),
+
=(1,k2-1),则k=2是
⊥
的( )
| a |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
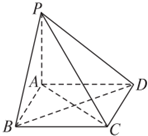 已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是