题目内容
12. 如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.
如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.(1)求证:平面PAC⊥平面PCD;
(2)若直线PC与平面PDE所成角的正弦值为$\frac{1}{4}$,求六棱锥P-ABCDEF高的大小.
分析 (Ⅰ)由CD⊥AC.CD⊥PA.得到CD⊥平面PAC.平面PAC⊥平面PCD
(Ⅱ)如图,分别以AC,AF,AP为x轴,y轴,z轴,建立空间直角坐标系A-xyz.
设AP=h(h>0).则P(0,0,h),C($\sqrt{3}$,0,0),D($\sqrt{3}$,1,0),E($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,0).
求出面PDE的一个法向量为$\overrightarrow{n}$=(x,y,z),sinθ=|cos<$\overrightarrow{PC}$,$\overrightarrow{n}$>|=$\frac{\sqrt{3}h}{2(h2+3)}$,解得h=$\sqrt{3}$.
解答 解:(Ⅰ)在正六边形ABCDEF中,CD⊥AC.
因为PA⊥底面ABCDEF,CD?平面ABCDEF,所以CD⊥PA.
又AC∩PA=A,所以CD⊥平面PAC.
因为CD?平面PCD,所以平面PAC⊥平面PCD.…(4分)
(Ⅱ)如图,分别以AC,AF,AP为x轴,y轴,z轴,建立空间直角坐标系A-xyz.
设AP=h(h>0).
则P(0,0,h),C($\sqrt{3}$,0,0),D($\sqrt{3}$,1,0),E($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,0).
$\overrightarrow{PC}$=($\sqrt{3}$,0,-h),$\overrightarrow{PD}$=($\sqrt{3}$,1,-h),$\overrightarrow{DE}$=(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0).
设面PDE的一个法向量为$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}$•$\overrightarrow{PD}$=0,$\overrightarrow{n}$•$\overrightarrow{DE}$=0,
所以$\left\{\begin{array}{l}{\sqrt{3}x+y-hz=0}\\{-\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\end{array}\right.$,取$\overrightarrow{n}$=(h,$\sqrt{3}$h,2$\sqrt{3}$).…(8分)
记直线PC与平面PDE所成的角为θ,则
sinθ=|cos<$\overrightarrow{PC}$,$\overrightarrow{n}$>|=$\frac{\sqrt{3}h}{2(h2+3)}$,
由$\frac{\sqrt{3}h}{2(h2+3)}$=$\frac{1}{4}$,解得h=$\sqrt{3}$.
所以六棱锥P-ABCDEF高为$\sqrt{3}$.…(12分)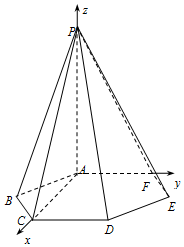
点评 本题考查了面面垂直的判定,空间向量在立体几何中的应用,属于中档题.

| x | 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
| y | 1.501 | 4.413 | 7.498 | 12.04 | 17.93 |
| A. | y=2x-1+1 | B. | $y=\frac{3}{2}{log_2}x$ | C. | $y=\frac{1}{2}{x^2}-\frac{1}{2}$ | D. | y=-2x-2 |
| A. | $\frac{25}{3}$π | B. | $\frac{28}{3}$π | C. | $\frac{28\sqrt{21}}{27}$π | D. | $\frac{25\sqrt{21}}{27}$π |
| A. | [-2,-1] | B. | (1,2) | C. | [-2,-1)∪(1,2] | D. | [-2,2] |
| A. | 1<x1<2,x1+x2<2 | B. | 1<x1<2,x1+x2<1 | C. | x1>1,x1+x2<2 | D. | x1>1,x1+x2<1 |
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.