在△ABC中.BC:AB=2:$\sqrt{3}$.∠B=30°.则∠C=( )A．30°B．45°C．60°D．75° 题目和参考答案——青夏教育精英家教网—

题目内容

19．在△ABC中，BC：AB=2：$\sqrt{3}$，∠B=30°，则∠C=（　　）

A．

30°

B．

45°

C．

60°

D．

75°

分析利用余弦定理与勾股定理的逆定理即可得出．

解答解：∵BC：AB=2：$\sqrt{3}$，不妨取a=2，c=$\sqrt{3}$．
∴b²=${2}^{2}+（\sqrt{3}）^{2}$-2×$2×\sqrt{3}×cos3{0}^{°}$=1．
∴b²+c²=a²，∴∠A=90°．
∴∠C=60°．
故选：C．

点评本题考查了余弦定理与勾股定理的逆定理，考查了推理能力与计算能力，属于中档题．

练习册系列答案

10．下面有段演绎推理：
“直线平行于平面，则该直线平行于平面内所有直线；
已知直线b?平面α，直线a?平面α，直线b∥平面α，
则直线b∥直线a”，则该推理中（　　）

7．曲线C的极坐标方程为：ρ=2cosθ，曲线T的参数方程为$\left\{\begin{array}{l}x=-t+1\\ y=2t+1\end{array}\right.$（t为参数），则曲线C与T的公共点有2个．

14．

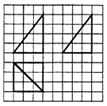如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（　　）

4．（2$\sqrt{x}$-$\frac{1}{\root{4}{x}}$）⁶的展开式的常数项是60（用数字作答）

11．

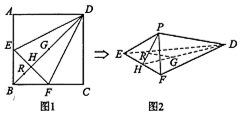如图l，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，点G，R分别在线段DH，HB上，且$\frac{DG}{GH}$=$\frac{BR}{RH}$．将△AED，△CFD，△BEF分别沿DE，DF，EF折起，使点A，B，C重合于点P，如图2所示，
（I）求证：GR⊥平面PEF；
（Ⅱ）若正方形ABCD的边长为4，求三棱锥P-DEF的内切球的半径．

8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+y²=1（a＞1）上一点M也在直线y=$\frac{1-{a}^{2}}{1+{a}^{2}}$上，M与N（0，1）两点所在直线过椭圆C的一个焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知P（x₀，y₀）是椭圆C上一点，若过点（$\frac{{x}_{0}}{3}$，-$\frac{{y}_{0}}{3}$）的直线与椭圆C有两个异于P的交点A，B，求证：PA丄PB．

9．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C：ρ²-4ρcosθ+1=0，直线l：$\left\{\begin{array}{l}{x=4+tsinα}\\{y=tcosα}\end{array}\right.$（t为参数，0≤α＜π）．
（1）求曲线C的参数方程；
（2）若直线l与曲线C相切，求直线l的倾斜角及切点坐标．

试题分类